Polynomials

Synopsis

• A polynomial p(x) in one variable x is an algebraic expression in x of the form
  p(x)= a_nXⁿ+a_n-1X^n-1+a_n-2X^_n-2+……+a₂X²+a1X + a0 , where 

1. a₀,a₁,a₂….an are constants
2. x is a variable
3. a₀,a₁,a₂….an are respectively the coefficients of xi
4. Each of  a_nXⁿ+a_n-1X^n-1+a_n-2X^n-2+……+a₂X²+a1X + a0  with an ≠0 ,is called a term of a polynomial.
     

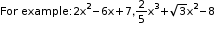
• Degree of a polynomial
  The highest power of the variable in a polynomial is called the degree of the polynomial.
  In case of more than one variable, degree is the highest sum of the powers of the variables.
• A polynomial with one term is called a monomial.
• A polynomial with two terms is called a binomial.
• A polynomial with three terms is called a trinomial.
• A polynomial with degree zero is called a constant polynomial. For example: 1, -3. The degree of non-zero constant polynomial is zero
• A polynomial of degree one is called a linear polynomial. It is of the form ax + b. For example: x - 2, 4y + 89, 3x - z.
• A polynomial of degree two is called a quadratic polynomial. It is of the form ax2 + bx + c. where a, b, c are real numbers and a ¹ 0 For example: x2 - 2x+ 5 etc.
• A polynomial of degree three is called a cubic polynomial and has the general form ax3 + bx2 + cx +d. For example: x3 - 2x2 -2x+5 etc.
• A bi-quadratic polynomial p(x) is a polynomial of degree four which can be reduced to quadratic polynomial in the variable z = x2 by substitution.
• The constant polynomial 0 is called the zero polynomial. Degree of zero polynomial is not defined.
• The value of a polynomial f(x) at x = p is obtained by substituting x = p in the given polynomial and is denoted by f(p).
• A real number ‘a’ is a zero or root of a polynomial p(x) if p (a) = 0.
• The number of real zeroes of a polynomial is less than or equal to the degree of polynomial.
• Finding a zero or root of a polynomial f(x) means solving the polynomial equation f(x) = 0.
• A non-zero constant polynomial has no zero.
• Every real number is a zero of a zero polynomial.

• Division of a polynomial by another polynomial
  If p(x) and g(x) are the two polynomials such that degree of p(x) ³  degree of g(x) and g(x) ≠ 0, then we can find polynomials q(x) and r(x) such that:
  p (x) = g(x) q(x) + r(x) 
  Where, r(x) =0 or degree of r(x) < degree of g(x).

• Remainder theorem
  Let p(x) be any polynomial of degree greater than or equal to one and let a be any real number. If p(x) is divided by the linear polynomial (x – a), then remainder is p(a).

1. If the polynomial p(x) is divided by (x + a), the remainder is given by the value of p (-a).
2. 
3. 

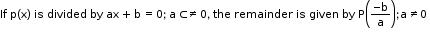
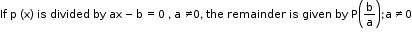
• Factor theorem
  Let p(x) is a polynomial of degree n ≥ 1 and a is any real number such that p(a) = 0, then (x – a) is a factor of p(x).

• Converse of factor theorem
  Let p(x) is a polynomial of degree n ≥ 1 and a is any real number. If (x – a) is a factor of p(x), then p(a) = 0.

1. (x + a) is a factor of a polynomial p(x) if p(–a) = 0.
2. (ax – b) is a factor of a polynomial p(x) if p(b/a) = 0.
3. (ax + b) is a factor of a polynomial p(x) if p(–b/a) = 0. 
4. (x – a)(x – b) is a factor of a polynomial p(x) if p(a) = 0 and p(b) = 0.

• For applying factor theorem, the divisor should be either a linear polynomial of the form (ax + b) or it should be reducible to a linear polynomial.

• A quadratic polynomial ax² + bx+ c is factorised by splitting the middle term by writing b as ps + qr such that (ps) (qr) = ac.
  Then, ax² + bx+ c = (px + q) (rx + s)

• An algebraic identity is an algebraic equation which is true for all values of the variables occurring in it.

• Some useful quadratic identities:

1. (x+y)² = X² + 2xy + y²
2. (x-y)² = X² - 2xy + y²
3. (x-y)(x+y)=x²-y²
4. (x-a)(x+b)=x²+(a+b)x+ab
5. (x+y+z)² = x²+y²+z²+2xy+2yz+2zx
   Here x, y, z are variables and a, b are constants.

• Some useful cubic identities:

1. (x+y)³ = x³ + y³ + 3xy(x+y)
2. (x-y)³ = x³ - y3- 3xy(x-y)
3. x3 +y³ =(x + y)(x²- xy + y²)
4. x3 - y³ = x -  y)(x²+ xy + y²)
5. x3 +y³ +z³ – 3xyz + (x+y+z) (x²+y²+z² – xy- yz –zx)
6. if x+y+z + 0 then x³ + y³ +z³ + 3xyz
   Here, x, y and z are variables.

• Synthetic Division for Factorisation
  The steps are as follows:

1. Write the coefficients in the descending powers of x in the first horizontal row.
   
2. The multiplier is obtained by putting the divisor x – a = 0
   
3. Write down the leading coefficient in the bottom row just below it.
   
4. Multiply ‘a’ with the value just written on the bottom row.
   
5. Add the two values and write the sum in the bottom row.
   
6. Repeat the steps (iii) and (iv) until the result turns out to be zero.
   For example: Divide 3x³- 2x²- 19x +22 by (x-2)
   Sol.
   
   Therefore,
   3x³- 2x² 19x +22 =(x-2) (3x²+4x-11)