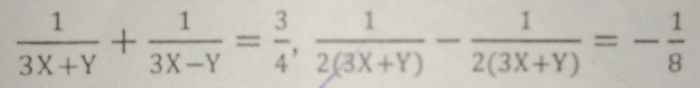CBSE Class 10 Answered

The given pair of linear equations are:

6x + 3y = 6xy

2x + 4y = 5xy

These are not linear equations in the variables x and y but can be reduced to linear equations by an appropriate substitution.

If we put x = 0 in either of the two equations, we get y = 0.

So, x = 0 and y = 0 form a solution of the given system of equations.

To find the other solutions, assume that .

On dividing each of the given equations by xy, we have:

The above equations become:

6u + 3v = 6                ...  (1)

2u + 4v = 5                 ... (2)

Multiplying equation (2) by 3, we get,

6u + 12v = 15                ... (3)

Subtracting equation (1) from equation (3), we have:

9v = 9 v = 1

From equation (1):

6u + 3v = 6 6u + 3.1 = 6 6u = 3 u = Hence, x = 1, y = 2