CBSE Class 10 Answered

Dear student

 

 

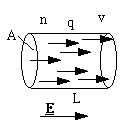
The sketch shows a conductor, length L, cross sectional area A. There are n charge carriers per cubic metre, each carrier having a charge q, and moving at an average speed v. The situation is analogous to the gravitational case except that we have charge q instead of mass m, and an electric field of magnitude E rather than a gravitational field of magnitude g. Inside the cylinder there are nAL charge carriers. The last charge carrier leaves the cylinder after a time t = L/v, so the total charge that leaves the cylinder per unit time is: I = (number of charge carriers)*(charge on each)/(time taken for them to leave) = (nAL)q/(L/v) = nAqv. Let's assume that the average speed v of the carriers is proportional to the electric field E that is moving them, ie write v = const.E. The electric field E is V/L where V is the difference in electrial potential across L, so v = const.E, = const.V/L,    so I = nAqv = n.A.const.E = const.V.nqA/L.   (3) Here we note that the current is: proportional to the number of charge carriers/cubic metre (n) proportional to the cross sectional area of the conductor (A) proportional to the magnitude of the field that moves them (E) proportional to the number of charge carriers/cubic metre of conductor (n)

(One must be careful about discussing the dependence on q. Experimentally, one usually cannot vary q. In cases where one can (eg if the charge carriers are ions in a solution), then changing q changes the constant of proportional ity as well.) We can now rearrange equation (3) to give

V/I = (L/A)(1/(nq.const.)),    which we can write as

V/I = (L/A)ρ = R

where R is the resistance of this piece of conducting material (whose units are ohms, Ω), and where ρ is the resistivity of the material (whose units are ohm metress, Ωm).

Alternatively, we can take the reciprocal of the terms in the above equation and write:

I/V = σ(A/L) = G

where G is the conductance of this piece of conductor, (G = 1/R), and where σ is the conductivity of the material,

σ = n.q.const = 1/ρ.

What if the current doesn't flow uniformly in a conductor? Then we should be interested in the current density or current per unit area: J = I/A. Combining the equations above gives the simplest form:

J = σE = E/ρ.

This is also the form that is closest to the way in which Ohm expressed his eponymous law originally. The current is parallel to E so in this case the equation has been written in vector form.

 

 

We hope that clarifies your doubt

 

Regards

Team

TopperLearning