Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

Show that the tangents to the curve y = 2x3 – 3 at the points where x = 2 and x = – 2 are parallel.
Asked by Topperlearning User | 07 Aug, 2014, 08:27: AM
answered-by-expert Expert Answer

The equation of the curve is y = 2x3 – 3     …(i)

Differentiating w.r.t. x, we get
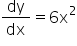
dy over dx equals 6 straight x squared 
Now,   m1 = Slope of the tangent at  x equals 2 space comma space open parentheses dy over dx close parentheses subscript x equals 2 end subscript equals 6 cross times left parenthesis 2 right parenthesis squared equals 24
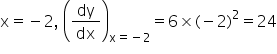
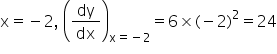
and,     m2 = Slope of the tangent at straight x equals minus 2 comma space open parentheses dy over dx close parentheses subscript straight x equals minus 2 end subscript equals 6 cross times left parenthesis minus 2 right parenthesis squared equals 24
Clearly, m1 = m2
Thus, the tangents to the given curve at the points where x = 2 and x = –2 are parallel.
Answered by | 07 Aug, 2014, 10:27: AM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 12-science - Maths
Find the angle of  intersection of 2 curve x^2y=2 and xy^2=4    
Asked by agarwalgolu318 | 13 Aug, 2020, 20:09: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Differentiate Sin x
Asked by givduf | 11 Jul, 2020, 09:00: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
find the eqation of tangent to curve 3x2-y2=8 which passthrough point 4/3,0
Asked by sonalchoudhary882 | 22 Oct, 2018, 00:22: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Show that the tangents to the curve y = 2x3 – 3 at the points where x = 2 and x = – 2 are parallel.
Asked by Topperlearning User | 07 Aug, 2014, 08:27: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
The slope of the curve 2y2 = ax2 + b at (1, – 1) is – 1. Find a, b
Asked by Topperlearning User | 07 Aug, 2014, 08:32: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
The slope of the normal to the curve x = 1 - a sin , y = b cos2 θ ï»¿ï»¿ï»¿ï»¿ï»¿ at q =straight pi over 2  is
Asked by Topperlearning User | 07 Aug, 2014, 09:19: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find the points on the curve y = x3 – 2x2 – x at which the tangent lines are parallel to the line y = 3x – 2.
Asked by Topperlearning User | 07 Aug, 2014, 09:58: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find the points on the curve y = x3 at which the slope of the tangent is equal to the y-coordinate of the point.
Asked by Topperlearning User | 07 Aug, 2014, 10:14: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find the point on the curve y = x3 – 11x + 5 at which the tangent has the equation y = x – 11.
Asked by Topperlearning User | 11 Aug, 2014, 10:06: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find the points on the curve 9y2 = x3 where normal to the curve makes equal intercepts with the axes.
Asked by Topperlearning User | 07 Aug, 2014, 12:43: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
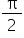Customised test packs for Teachers, Parents, and Students. Click here for details!
×