CBSE Class 12-science Answered
Find the point on the curve y = x3 – 11x + 5 at which the tangent has the equation y = x – 11.
Asked by Topperlearning User | 11 Aug, 2014, 10:06: AM
Let the required point be P(x1, y1), since (x1, y1) lies on y = x3 – 11x + 5.
y1 = 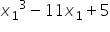 …(i)
…(i)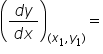
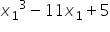 …(i)
…(i)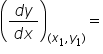
Now, y = x3 – 11x + 5
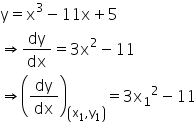
Since the line y = x – 11 is tangent at the point (x1, y1). Therefore,
Slope of the tangent at (x1, y1) = (Slope of the line y = x – 11).
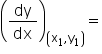 (Slope of the line x – y – 11 = 0)
(Slope of the line x – y – 11 = 0)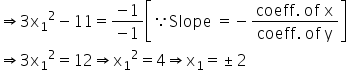
Now,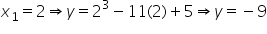 [Using (i)]
[Using (i)]
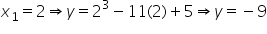 [Using (i)]
[Using (i)]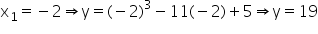 [Using (i)]
[Using (i)]So, two points are (2, –9) and (–2, 19). Of these two points (–2, 19) does not lie on y = x – 11. Therefore, the required point is (2, – 9).
Answered by | 11 Aug, 2014, 12:06: PM
Concept Videos
CBSE 12-science - Maths
Asked by agarwalgolu318 | 13 Aug, 2020, 20:09: PM
CBSE 12-science - Maths
Asked by givduf | 11 Jul, 2020, 09:00: AM
CBSE 12-science - Maths
Asked by sonalchoudhary882 | 22 Oct, 2018, 00:22: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 08:27: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 08:32: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 09:19: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 09:58: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 10:14: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 11 Aug, 2014, 10:06: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 12:43: PM




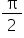 is
is