CBSE Class 12-science Maths Applications of Derivatives
- Find the angle of intersection of 2 curve x^2y=2 and xy^2=4
- Differentiate Sin x
- find the eqation of tangent to curve 3x2-y2=8 which passthrough point 4/3,0
- Show that the tangents to the curve y = 2x3 – 3 at the points where x = 2 and x = – 2 are parallel.
- The slope of the curve 2y2 = ax2 + b at (1, – 1) is – 1. Find a, b
-
The slope of the normal to the curve
x = 1 - a sin
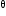, y = b cos2 θ  at q =
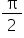is
- Find the points on the curve y = x3 – 2x2 – x at which the tangent lines are parallel to the line y = 3x – 2.
- Find the points on the curve y = x3 at which the slope of the tangent is equal to the y-coordinate of the point.
- Find the point on the curve y = x3 – 11x + 5 at which the tangent has the equation y = x – 11.
- Find the points on the curve 9y2 = x3 where normal to the curve makes equal intercepts with the axes.
