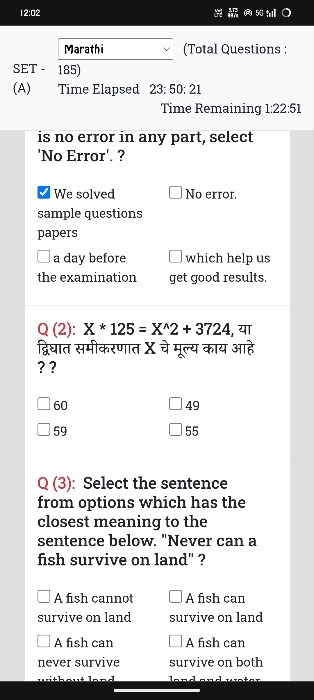
CBSE Class 10 Answered
Please solve this question

Asked by vikasg13.hardware | 28 Jun, 2018, 06:03: AM
Let y = x2 + 5 and y = 7[x]
Minimum value of y in equation y = x2 + 5 is 5.
Minimum value of y = 7[x] is less than zero for negative values of x
Hence, roots are in the first quadrant.
Consider curve for 0 < x < 1
The value of x2 + 5 is greater than 5 and 7[x] is zero.
Similarly you can solve it in the interval (1, 2), (2, 3) ....
you will get
the sum of the squares for 1 < x < 2 is 2.
The sum of the squares for 4 < x < 5 is 23.
The sum of the squares for 5 < x < 6 is 30.
the sum of the squares for 6 < x < 7 is 37.
The sum of the squares is 92
Answered by Sneha shidid | 06 Jul, 2018, 09:31: AM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by raopaidi | 25 Apr, 2024, 04:06: PM
CBSE 10 - Maths
Asked by aditikaldate7 | 21 Apr, 2024, 03:16: PM
CBSE 10 - Maths
Asked by pathaksuman622 | 21 Apr, 2024, 11:56: AM
CBSE 10 - Maths
Asked by yalagondanikhil | 16 Apr, 2024, 12:25: PM
CBSE 10 - Maths
Asked by rrajansinghakb199 | 08 Apr, 2024, 05:12: PM
CBSE 10 - Maths
Asked by nagalaxmidurgarao937 | 08 Apr, 2024, 01:42: PM
CBSE 10 - Maths
Asked by mraniruddha03 | 02 Apr, 2024, 06:44: PM
CBSE 10 - Maths
Asked by muttenenimalleswarrao | 29 Mar, 2024, 08:32: PM
CBSE 10 - Maths
Asked by pathakvaishnavi9139 | 23 Mar, 2024, 10:45: AM