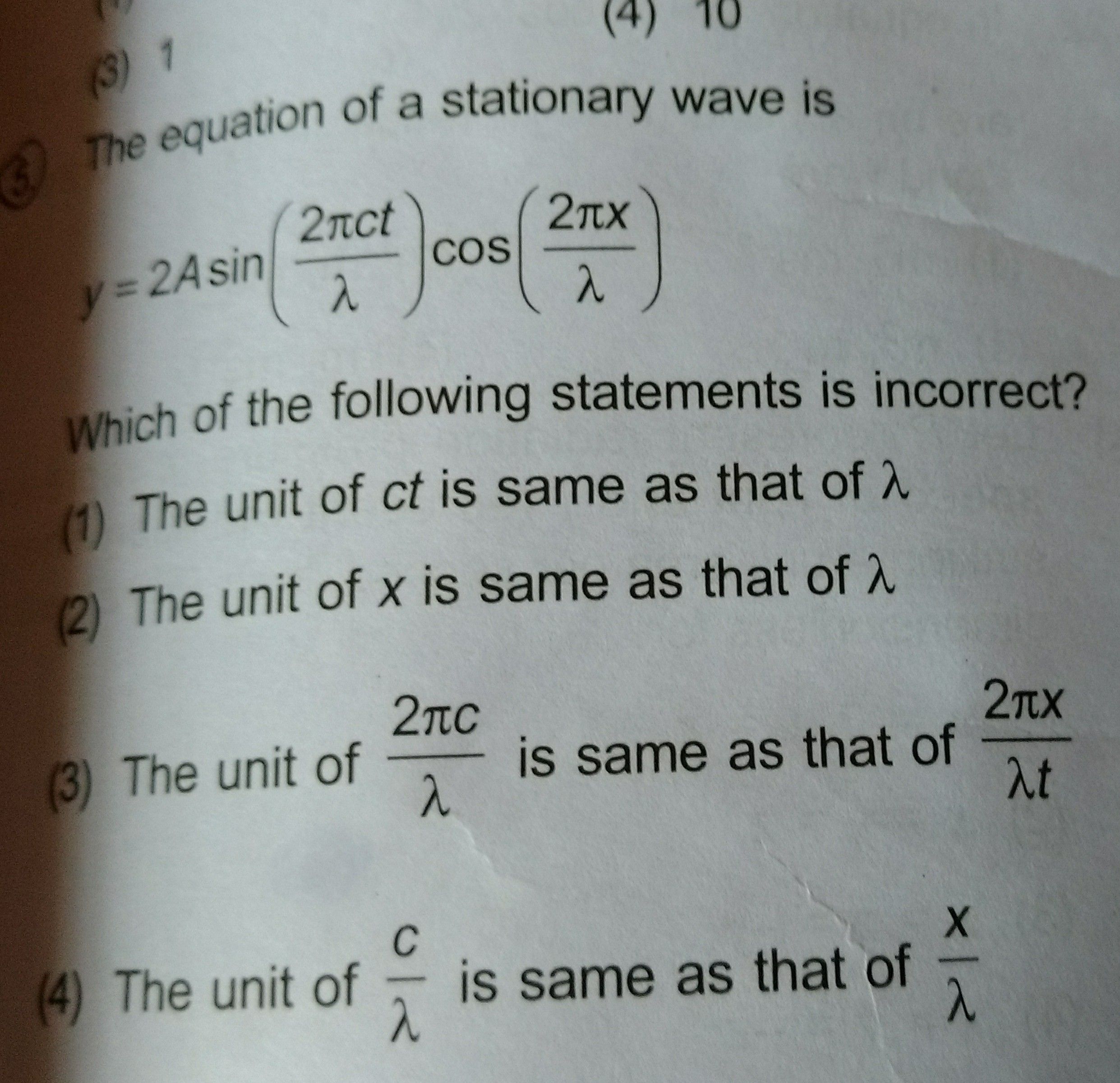CBSE Class 11-science Answered
Please refer to the uploaded image for the doubt.
[In the image, length of the open pipe=0..6m] // *SORRY FOR BAD QUALITY* //
Asked by arjunsah797 | 17 May, 2022, 13:19: PM
Expert Answer
Part (a)
Let us now consider a system of an air column of finite length in a tube and both the ends of tube are open .
In such a system suppose that we send a continuous sinusoidal wave of a certain frequency, say,
toward the right. When the wave reaches the right end, it gets reflected and begins to travel back.
toward the right. When the wave reaches the right end, it gets reflected and begins to travel back.
The left-going wave then overlaps the wave, travelling to the right.
When the left-going wave reaches the left end, it gets reflected again and the newly reflected
wave begins to travel to the right, overlapping the left-going wave. This process will continue and, therefore, very soon
we have many overlapping waves, which interfere with one another. In such a system, at any point x and at any time t,
we have many overlapping waves, which interfere with one another. In such a system, at any point x and at any time t,
there are always two waves, one moving to the left and another to the right.
The combined wave equation that is obtained from principle of superposition in both ends are open pipe is given as
y (x, t) = [ 2a sin (kx + π/2 ) ] cos ωt
where the square bracketted term gives amplitude of oscillation of air particles as a function of x ,
a is amplitude of individual wave, k = 2π/λ is wave vector , ω = 2πf is angular frequency and f is frequecy of wave.
--------------------------------------------------------------------------------
Part (b)
--------------------------------------------------------------------------------------
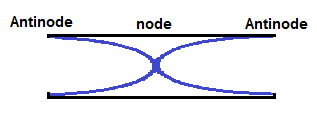
Part (c)
Wavelength λ of standing wave is determined from λ/2 = l , where l is length of pipe
Hence, wavelength λ = ( 2 l ) = ( 2 × 0.6 ) m = 1.2 m
since node is at a distance x = 0.3 m from left open end, at x = 0.15 m direction of oscillation of air particles
is towards left from its equilibrium position.
phase φ1 at x = 0.1 m is determined as follows
φ1 = ( kx + π/2 ) = [ (2π / λ ) x + π/2 ] = [ (2π / 1.2 ) 0.1 + π/2 ] = ( 2π / 3 )
phase φ2 at x = 0.2 m is determined as follows
φ2 = ( kx + π/2 ) = [ (2π / λ ) x + π/2 ] = [ (2π / 1.2 ) 0.2 + π/2 ] = ( 5π / 6 )
Phase difference = φ2 - φ1 = ( 5π / 6 ) - ( 2π / 3 ) = ( π / 6 )
Answered by Thiyagarajan K | 17 May, 2022, 15:46: PM
CBSE 11-science - Physics
Asked by emad.amd | 21 Mar, 2024, 12:00: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by arjunsah797 | 17 May, 2022, 13:19: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by lakshmiks703 | 17 Apr, 2022, 19:23: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by Umeshlochab80 | 12 May, 2021, 21:24: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by ks076345 | 22 Mar, 2021, 09:20: AM
ANSWERED BY EXPERT
CBSE 11-science - Physics
Asked by lovemaan5500 | 29 Jan, 2019, 11:26: AM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by lovemaan5500 | 29 Jan, 2019, 11:25: AM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by lovemaan5500 | 29 Jan, 2019, 11:25: AM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by lovemaan5500 | 29 Jan, 2019, 11:24: AM
ANSWERED BY EXPERT