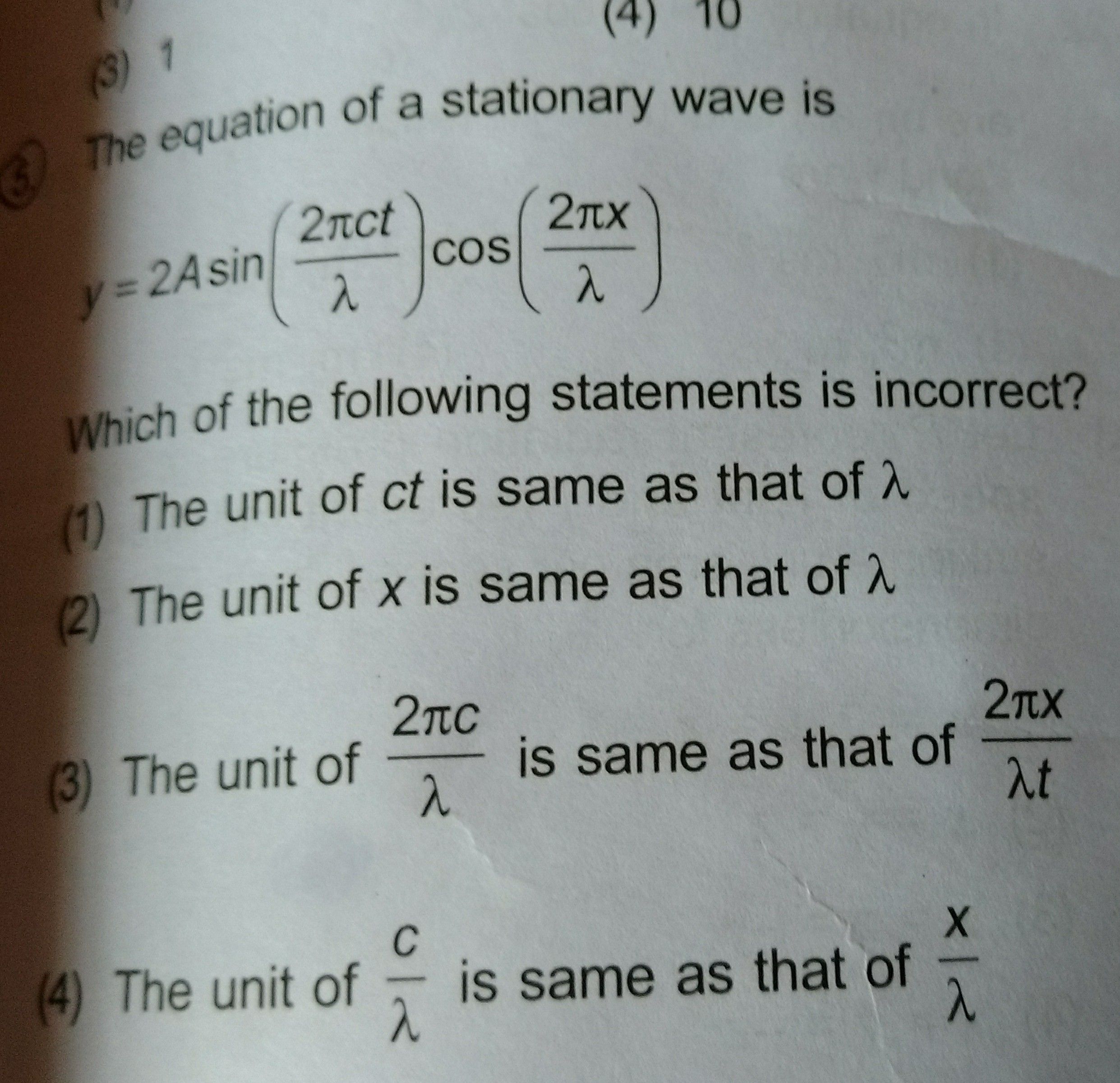CBSE Class 11-science Answered
how to prove that the frequencies produced in the string are in the ratio 1:2:3
Asked by lakshmiks703 | 17 Apr, 2022, 07:23: PM
Expert Answer
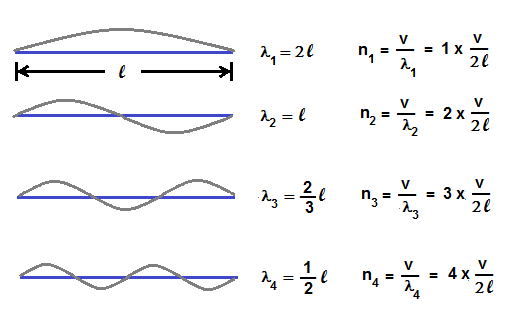
When a stretched string vibrates in fundamenetal mode or first harmonic , wavelength λ1 = 2 l as shown in figure ,
where l is length of string. If v is the speed of wave then frequency n1 of fundamental mode , n1 = v / λ1 = 1 × ( v / 2l ) .
When a stretched string vibrates in second harmonic , wavelength λ2 = l as shown in figure ,
Then frequency n2 of second harmonic , n2 = v / λ2 = 2 × ( v / 2l ) .
Similarly , frequency n3 of third harmonic , n3 = v / λ3 = 3 × ( v / 2l ) .
Frequency n4 of fourth harmonic , n4 = v / λ4 = 4 × ( v / 2l ) .
Hence frequencies of vibration in stretched string = n1 : n2 : n3 : n4 = 1 × ( v / 2l ) : 2 × ( v / 2l ) : 3 × ( v / 2l ) : 4 × ( v / 2l ) .
n1 : n2 : n3 : n4 = 1 : 2 : 3 : 4 .
Answered by Thiyagarajan K | 18 Apr, 2022, 09:06: AM
CBSE 11-science - Physics
Asked by emad.amd | 21 Mar, 2024, 12:00: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by arjunsah797 | 17 May, 2022, 01:19: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by lakshmiks703 | 17 Apr, 2022, 07:23: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by Umeshlochab80 | 12 May, 2021, 09:24: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by ks076345 | 22 Mar, 2021, 09:20: AM
ANSWERED BY EXPERT
CBSE 11-science - Physics
Asked by lovemaan5500 | 29 Jan, 2019, 11:26: AM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by lovemaan5500 | 29 Jan, 2019, 11:25: AM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by lovemaan5500 | 29 Jan, 2019, 11:25: AM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by lovemaan5500 | 29 Jan, 2019, 11:24: AM
ANSWERED BY EXPERT
