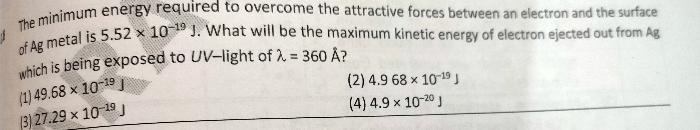CBSE Class 11-science Answered
To explain the phenomena of ‘Black body radiation’ and ‘Photoelectric effect’, Max Plank in 1900, put forward a theory which is known after his name as Plank’s quantum theory.
The main points of this theory are as follows:
(i) The radiant energy is emitted or absorbed not continuously but discontinuously in the form of small discrete packets of energy. Each such packet of energy is called a ‘quantum’. In case of light, the quantum of energy is called a ‘photon’.
(ii) The energy of each quantum is directly proportional to the frequency of the radiation, that is
E ∝ ν or E = hν
where is h is proportionality constant, called Plank’s constant. Its value is approximately equal to 6.626×10-27 erg sec or 6.626×10-34 joule sec.
(iii) The total amount of energy emitted or absorbed by a body will be some whole number quanta.
Hence, E = nhν where n is any integer.