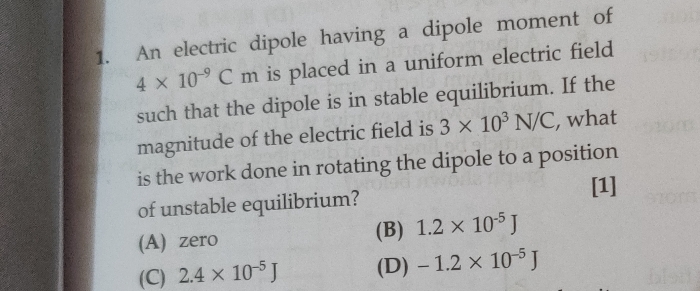Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

Obtain the ratio of Electric field formed by an ideal dipole at points lying on axial and equatorial axis.
Asked by avaneesh1162 | 12 Jun, 2021, 11:06: AM
answered-by-expert Expert Answer
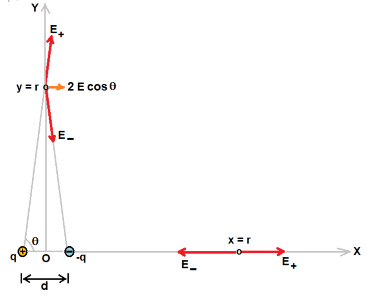
Let a dipole consists of charges +q and -q that are separated by a distance d is placed at origin of
X-Y coordinate system so that mid point of dipole coinicides with origin.
 
Electric field at a point x = r on x-axis is given as
 
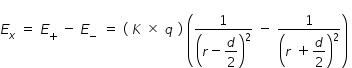
begin mathsize 14px style E subscript x space equals space E subscript plus space minus space E subscript negative space space end subscript equals space left parenthesis space K space cross times space q space right parenthesis space open parentheses 1 over open parentheses r minus begin display style d over 2 end style close parentheses squared space minus space 1 over open parentheses r space plus begin display style d over 2 end style close parentheses squared close parentheses space end style 

 
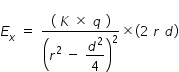begin mathsize 14px style E subscript x space equals space fraction numerator left parenthesis space K space cross times space q space right parenthesis over denominator open parentheses r squared space minus space begin display style d squared over 4 end style close parentheses squared end fraction cross times left parenthesis 2 space r space d right parenthesis end style ..................................(1)

 
Where K = 1/ (4πεo ) is Coulomb's constant
 
if we consider dipole moment p = ( q × d )   and  r >> d/2 , then eqn.(1) is written as
 
Ex  = K × [ ( 2 p ) / r3  ]  ............................ (2)
 
Electric field at a point y = r on y-axis is given as
 
Ey = 2 E cosθ  .................................(3)
 
Where  E is given as
begin mathsize 14px style E space equals space E subscript plus space equals space E subscript minus space equals space K space cross times fraction numerator q over denominator open parentheses r squared space plus space begin display style d squared over 4 end style close parentheses end fraction end style
Hence we get Ey as  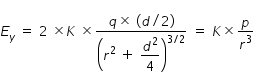 ,  begin mathsize 14px style E subscript y space equals space 2 space cross times K space cross times fraction numerator q cross times space left parenthesis d divided by 2 right parenthesis over denominator open parentheses r squared space plus space begin display style d squared over 4 end style close parentheses to the power of 3 divided by 2 end exponent end fraction space equals space K cross times p over r cubed end style 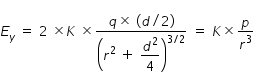.........................(4)

In above expression , we used the approximation r >> d  and  dipole moment p = ( q × d ) 
 
From eqn.(2) and eqn.(4) , we get  ( Ex / Ey )  = 2 
Answered by Thiyagarajan K | 12 Jun, 2021, 02:59: PM

Concept Videos

Multiple Choice Questions Practice Test Subjective Questions Webinar Subjective Questions Pre Board Assessment
Answered Unanswered My Questions My Answers
CBSE 12-science - Physics
Please solve this question
question image
Asked by shinghip6 | 17 Jul, 2022, 04:36: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
Derive an expression for the torque acting on an electric dipole kept in a uniform electric field. When is this torque maximum? What will happen if the field were not uniform?
Asked by bolojubakesri47 | 15 Jul, 2022, 06:15: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
calculate the electric field due to the electric dipole of length 2 cm having charge 4 microcoulomb at an angle of minus 60 degree for the direction of electric dipole moment 1 meter for the center to the dipole
Asked by surajsinghrajput4691 | 16 May, 2022, 12:20: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
CALCULATE ELECTIC FEILD INTENSITY DUE TO DATIPOLE OF LENTH 10 CM HAVING CHARGE 5000MICROCOULUMB AT POINT ON AXIS OF LENTH 20 CM FROM ONE OF THE CHARGE        
Asked by CHITTIBOMMAPARDHANADH | 06 Sep, 2021, 02:27: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
An electric dipole with dipole moment 4×10-9cm is aligned at 30° with the direction of a uniform electric field of magnitude 5×104N/C. Calculate the magnitude of torque acting on the dipole?
Asked by krishnamm7000 | 25 Jun, 2021, 07:30: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
Two short electic dipoles of moment P and 8P are placed in opposite direction on a line at a distance of 15cm. The electic will be zero at point between the dipoles wose distance from the dipole of moment P is 
Asked by KRISHPATEL.soc | 20 Jun, 2021, 02:02: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
Obtain the ratio of Electric field formed by an ideal dipole at points lying on axial and equatorial axis.
Asked by avaneesh1162 | 12 Jun, 2021, 11:06: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
Determine electric field at a point p for two identical dipole placed along x and y axis with dipole moment p and angle  45°
Asked by manishamalakar52 | 20 Apr, 2021, 09:14: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
the electric field at a point on the axial line at a distance of 10cm from the centre of an electric dipole is 3×10³NC·¹ in air while at a diatance of 15cm,the electric field is 2×10³NC·¹ Calculate the length of an electric dipole. 3×10³NC·¹
Asked by Rinfeli567 | 07 Jul, 2020, 07:10: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
An electric dipole moment 4x10^-9 cm is aligned at 30°with the direction of a uniform electric field of magnitude 5x10^4 NC^-1.calculate the magnitude of the torque acting on the dipole? 
Asked by mayaunni486 | 06 Jul, 2020, 11:26: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt