Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

calculate the electric field due to the electric dipole of length 2 cm having charge 4 microcoulomb at an angle of minus 60 degree for the direction of electric dipole moment 1 meter for the center to the dipole
Asked by surajsinghrajput4691 | 16 May, 2022, 12:20: AM
answered-by-expert Expert Answer
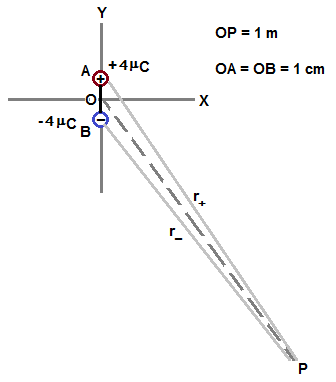
Let the dipole is at origin of cartesian coordinate system as shown in figure.
 
electric field at P is given as
 
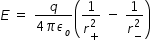
begin mathsize 14px style E space equals space fraction numerator q over denominator 4 pi epsilon subscript o end fraction open parentheses fraction numerator 1 over denominator r subscript plus superscript 2 end fraction space minus space fraction numerator 1 over denominator r subscript minus superscript 2 end fraction close parentheses end style
 
where q is magnitude of individual charge of dipole , r+ is ditsance between positive charge and point P , 
r- is ditsance between negative charge and point Pand εo is permittivity of free space .
 
distance r+ is determined as follows using cosine rule
 
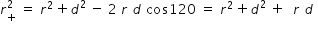
begin mathsize 14px style r subscript plus superscript 2 space equals space r to the power of 2 to the power of space end exponent plus d squared space minus space 2 space r space d space cos 120 space equals space r to the power of 2 to the power of space end exponent plus d squared space plus space space r space d space end style
where r is distance from origin to point P and 2d is length of dipole

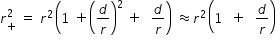
begin mathsize 14px style r subscript plus superscript 2 space equals space r to the power of 2 to the power of space end exponent open parentheses 1 space plus stretchy left parenthesis d over r stretchy right parenthesis squared space plus space space d over r close parentheses space almost equal to r to the power of 2 to the power of space end exponent stretchy left parenthesis 1 space space plus space space d over r stretchy right parenthesis space end style
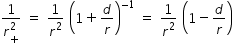
begin mathsize 14px style fraction numerator 1 over denominator r subscript plus superscript 2 end fraction space equals space 1 over r squared space open parentheses 1 plus d over r close parentheses to the power of negative 1 end exponent space equals space 1 over r squared space open parentheses 1 minus d over r close parentheses end style
 
similarly we get
 
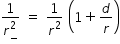
begin mathsize 14px style fraction numerator 1 over denominator r subscript minus superscript 2 end fraction space equals space 1 over r squared space open parentheses 1 plus d over r close parentheses end style
 
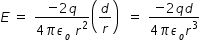
begin mathsize 14px style E space equals space fraction numerator negative 2 q over denominator 4 pi epsilon subscript o space r squared end fraction open parentheses d over r close parentheses space space equals space fraction numerator negative 2 q d over denominator 4 pi epsilon subscript o r cubed end fraction end style
let us substitute values
 
1/(4πεo ) = 9 × 109 N m2 C-2   , q = 4 × 10-6 C and d =1 cm
 
E = - ( 9 × 109 × 2 × 4 × 10-6 × 0.01 ) / 13 = -720 N
Answered by Thiyagarajan K | 16 May, 2022, 09:57: AM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 12-science - Physics
explain
question image
Asked by ranadeb8090 | 19 Apr, 2024, 03:32: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
give me answe
question image
Asked by sachin.sondur2012 | 07 Feb, 2024, 11:26: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
Define Electric dipole. Derive an expression for electric feild intensity at a point situated at a distance r from electric dipole
Asked by millionairekishan | 25 Jan, 2024, 12:34: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
abcd
question image
Asked by mahantabibhutibhusan261 | 06 Nov, 2023, 09:04: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
Please solve this question
question image
Asked by shinghip6 | 17 Jul, 2022, 04:36: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
Derive an expression for the torque acting on an electric dipole kept in a uniform electric field. When is this torque maximum? What will happen if the field were not uniform?
Asked by bolojubakesri47 | 15 Jul, 2022, 06:15: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
calculate the electric field due to the electric dipole of length 2 cm having charge 4 microcoulomb at an angle of minus 60 degree for the direction of electric dipole moment 1 meter for the center to the dipole
Asked by surajsinghrajput4691 | 16 May, 2022, 12:20: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
CALCULATE ELECTIC FEILD INTENSITY DUE TO DATIPOLE OF LENTH 10 CM HAVING CHARGE 5000MICROCOULUMB AT POINT ON AXIS OF LENTH 20 CM FROM ONE OF THE CHARGE        
Asked by CHITTIBOMMAPARDHANADH | 06 Sep, 2021, 02:27: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
An electric dipole with dipole moment 4×10-9cm is aligned at 30° with the direction of a uniform electric field of magnitude 5×104N/C. Calculate the magnitude of torque acting on the dipole?
Asked by krishnamm7000 | 25 Jun, 2021, 07:30: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
Two short electic dipoles of moment P and 8P are placed in opposite direction on a line at a distance of 15cm. The electic will be zero at point between the dipoles wose distance from the dipole of moment P is 
Asked by KRISHPATEL.soc | 20 Jun, 2021, 02:02: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×