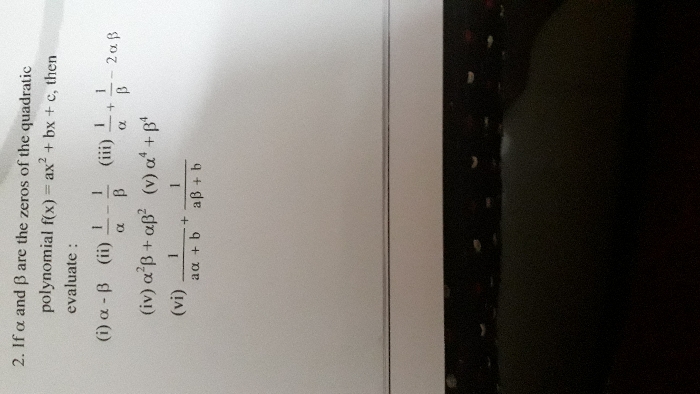Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

Let S be the area of the slant height of a right circular cone,V the volume , h the height and alpha is the  semi vertical angle then prove that S=pie×h3×sin alpha/cos2alpha and V=1/3 pie ×h3×tan2alpha
Asked by rushabhjain.a | 01 Dec, 2018, 05:47: PM
answered-by-expert Expert Answer

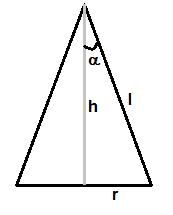
radius r of the base of the cone is given by,  r = h×tanα
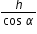
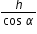
slant height l = begin mathsize 12px style fraction numerator h over denominator cos space alpha end fraction end style
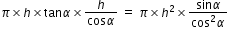
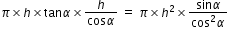
Surface Area S = π × r × l = begin mathsize 12px style pi cross times h cross times tan alpha cross times fraction numerator h over denominator cos alpha end fraction space equals space pi cross times h squared cross times fraction numerator sin alpha over denominator cos squared alpha end fraction end style
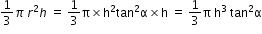
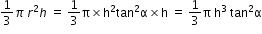
Volume V = begin mathsize 12px style 1 third pi space r squared h space equals space 1 third straight pi cross times straight h squared tan squared straight alpha cross times straight h space equals space 1 third straight pi space straight h cubed space tan squared straight alpha end style
Answered by Thiyagarajan K | 01 Dec, 2018, 09:48: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
2x² - 5x + 3 = 0  
Asked by biswajitgope404 | 09 May, 2024, 09:30: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
solve it
question image
Asked by vishalgunjan13 | 09 May, 2024, 02:13: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
solutions
question image
Asked by mukammilh19 | 07 May, 2024, 02:28: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
3x-5y-4=0...9x=2y+7
question image
Asked by laxman44verma | 01 May, 2024, 09:46: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
if p(X) = 2x^2-3x+4 find Alfa+beta
Asked by dagardisha39 | 28 Apr, 2024, 12:58: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
cos80÷ sin10+cos59• cosec31
Asked by raopaidi | 25 Apr, 2024, 04:06: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
2/x+2/3y=1/6; 3/x+2/y=0
Asked by aditikaldate7 | 21 Apr, 2024, 03:16: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
ABCD is a rectangle in which diagonal AC is equals to 17 cm angle BCA is equals to thitha and sin theta is equals to 8/17 find the area of rectangle ABCDE (ii) the perimeter of rectangle ABCD
Asked by pathaksuman622 | 21 Apr, 2024, 11:56: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
PQ is a chord of length 8 cm to a circle of radius 5 cm. The tangents P and Q intersect at a point T. Find the length of the tangent TP.
Asked by yalagondanikhil | 16 Apr, 2024, 12:25: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
if one of the zeroes of quadratic polynomial F(x) = 4x² - 8kx - 9 is equal in magnitude but opposite in sign, find K
Asked by rrajansinghakb199 | 08 Apr, 2024, 05:12: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×