Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

if the unit of length and mass be doubled then the numerical value of w. r. t present value of universal gravitational constant will become
Asked by suhani.pare | 28 Jun, 2021, 09:03: PM
Expert Answer
Let us consider gravitational force of attraction F  between two objects of equal mass m that are sepearted by a distance d
 
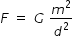
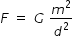
Then we have ,   begin mathsize 14px style F space equals space G space m squared over d squared end style  
where G is universal gravitational constant
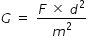
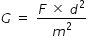
Hence Gravitational constant G is written as  ,  begin mathsize 14px style G space equals space fraction numerator F space cross times space d squared over denominator m squared end fraction end style
Dimensions of force F = [ M L S-2 ]
 
Dimension of distance d = [ L ]
 
Dimension of mass m = [ M ]
 
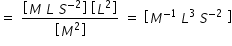
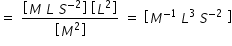
Dimension of G  begin mathsize 14px style equals space fraction numerator open square brackets M space L space S to the power of negative 2 end exponent close square brackets space open square brackets L squared close square brackets over denominator open square brackets M squared close square brackets end fraction space equals space open square brackets M to the power of negative 1 end exponent space L cubed space S to the power of negative 2 end exponent space close square brackets end style
if unit of mass is doubled, then present quantity of mass becomes (1/2) of modified mass .
 
Since gravitational constant G is inversely prportional to mass ,  G will be increased by a factor 2
 
if unit of length is doubled, then present length becomes (1/2) of modified length .
 
Since gravitational constant G is directly prportional to cube of distance ,  G will be decreased by a factor (1/2)3 = 1/8
 
Hence , modified universal gravitational constant G' = (2/8) G = (1/4)G
 
Modified universal gravitational constant G' = 0.25 × 6.674 × 10-11 = 1.668 × 10-11 N' (m' )2 (kg')-2
 
( Where N' , m' and kg' are modified Newton , modified metre and modified kg in new units system )
 
Answered by Thiyagarajan K | 28 Jun, 2021, 10:07: PM

Concept Videos

Multiple Choice Questions Practice Test Subjective Questions Webinar Subjective Questions Pre Board Assessment
Answered Unanswered My Questions My Answers
CBSE 11-science - Physics
signify digit of 0.7048
Asked by manthansakhare050 | 18 Dec, 2022, 01:54: AM
ANSWERED BY EXPERT
CBSE 11-science - Physics
For class 12 physics cbse board will they ask us dimensional formula for anything?will there be questions expected as to write the dimensional formulas?  
Asked by adibafatima2004 | 11 Sep, 2021, 08:02: PM
ANSWERED BY EXPERT
CBSE 11-science - Physics
if the unit of length and mass be doubled then the numerical value of w. r. t present value of universal gravitational constant will become
Asked by suhani.pare | 28 Jun, 2021, 09:03: PM
ANSWERED BY EXPERT
CBSE 11-science - Physics
check the dimensional accuracy of n=1/2L*rootT/M
Asked by gopikagopakumar43 | 13 Dec, 2020, 12:56: PM
ANSWERED BY EXPERT
CBSE 11-science - Physics
plzz solve this my que
Asked by sagarrc1564 | 11 Sep, 2020, 01:33: PM
ANSWERED BY EXPERT
CBSE 11-science - Physics
Check the correctness of the equation, When the rate of flow of a liquid having a coefficient of  viscosity ‘η’ through a capillary tube of length ‘l’ and radius ‘a’ under true pressure head ‘p’ is given by 𝑑𝑉 ÷ 𝑑t = 𝜋𝑝𝑎^4 ÷ 8lη
Asked by hemaborate26 | 13 Jul, 2020, 09:56: PM
ANSWERED BY EXPERT
CBSE 11-science - Physics
Please undoubt the question . Image is attached.
Asked by hemaborate26 | 12 Jul, 2020, 08:18: PM
ANSWERED BY EXPERT
CBSE 11-science - Physics
if area (a) velocity (v) and density(p)are base units,then whats the dimensinal formula of force represented as
Asked by spy20072004 | 08 Jul, 2020, 10:37: PM
ANSWERED BY EXPERT
CBSE 11-science - Physics
Q) How many significant Figures are there in ₹1000 and 1000pens? Please answer along with concept.
Asked by abhishekverma0300 | 03 Jul, 2020, 08:29: PM
ANSWERED BY EXPERT
CBSE 11-science - Physics
using dimensional analysis, the accuracy of relation 𝒗 = 𝒌𝒏 𝒓𝒅 , v is Velocity, k is constant, n is coefficient of viscosity [ML-1 T -1 ] , r is radius and d is density.
Asked by poo.pathak.orra | 06 May, 2020, 04:55: PM
ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt