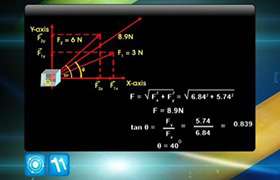
CBSE Class 11-science Answered
Find the resultant and the direction of resultant of two vectors A and B with angle  between them
between them
 between them
between them
Asked by neerajchauhan000000 | 23 Sep, 2021, 03:33: PM
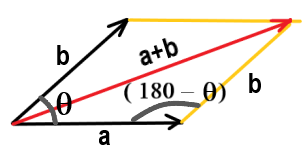
Figure shows two vectors a and b . Let θ be the angle between vectors.
By law of parallelogram, resultant vector (a+b) is the diagaonal of the parallelogram
formed by the vectors a and b as sides as shown in figure.
Magnitude of resultant (a+b) is determined using law of cosines using the triangle
formed by vector a , vector b and the resultant (a+b)
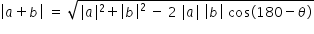
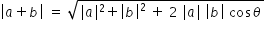
Answered by Thiyagarajan K | 24 Sep, 2021, 12:55: AM
Concept Videos
CBSE 11-science - Physics
Asked by vinitdubey7735 | 14 Mar, 2024, 11:21: AM
CBSE 11-science - Physics
Asked by dhanshreekansyakar | 09 Jan, 2024, 11:57: AM
CBSE 11-science - Physics
Asked by banhisikhapanda49 | 07 Nov, 2023, 10:42: PM
CBSE 11-science - Physics
Asked by preethiprithivi05 | 21 Feb, 2023, 09:28: PM
CBSE 11-science - Physics
Asked by rk274268 | 05 Aug, 2022, 01:19: PM
CBSE 11-science - Physics
Asked by Kattaithihaas | 24 Jul, 2022, 01:23: PM
CBSE 11-science - Physics
Asked by pawankumardas15492 | 22 Jul, 2022, 10:24: PM
CBSE 11-science - Physics
Asked by nutankumari95074 | 11 Jun, 2022, 05:24: PM
CBSE 11-science - Physics
Asked by kaziryan.05 | 13 Apr, 2022, 09:01: PM
CBSE 11-science - Physics
Asked by aditya000ghoderao | 19 Jan, 2022, 05:05: AM