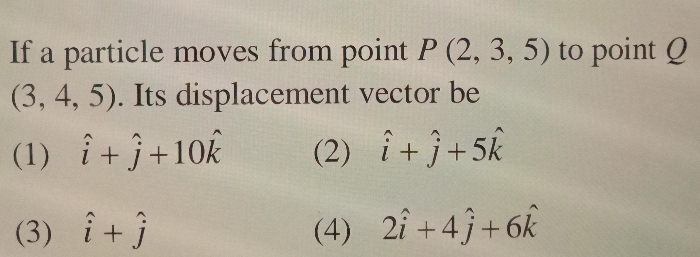CBSE Class 11-science Answered

For the simplicity and consistency across the 3 equations, v(t) has been represented as v, v(0) has been represented as u and x has been represented as s. 

FIRST EQUATION OF MOTION

a=(v-u)/t

at = v-u

=> v-u = at

=> v= u + at (1)

This is Newton's First equation of motion. As you can you see, we can use this equation to calculate the velocity of a body which underwent an acceleration of a m/s for a time period of t seconds, provided we know the initial velocity of the body. Initial velocity i.e. u is the velocity of the body just before the body started to accelerate i.e. the velocity at t=0.

SECOND EQUATION OF MOTION

velocity = distance traveled / time taken

average velocity = (u+v)/2

.: (u+v)/2 = s/t

s = [(u+v)/2]t

From equation (1) we have v=u+at, substituting this in the above equation for v, we get

s = [(u+u+at)/2]t

=> s = [(2u+at)/2]t

=> s = [(u + (1/2)at)]t

=> s = ut + (1/2)at2 - (2)

This is Newton's second equation of Motion. This equation can be used to calculate the distance traveled by a body moving with a uniform acceleration in a time t. Again here, if the body started from rest, then we shall substitute u=0 in this equation

THIRD EQUATION OF MOTION

We start with squaring equation (1). Thus we have

v² = (u+at)²

=> v² = u² + a2t2 + 2uat

=> v² = u² + 2uat + a2t2

=> v² = u² + 2a(ut + (1/2)at2)

now, using equation 2 we have

=> v² = u² + 2as - (3)

As you can see, the above equation gives a relation between the final velocity v of the body and the distance s traveled by the body.

Thus, we have the the three Newton's equations of Motion as

1) v= u + at

2) s = ut + (1/2)at²

3) v² = u² + 2as