CBSE Class 11-science Answered
check the dimensional accuracy of n=1/2L*rootT/M
Asked by gopikagopakumar43 | 13 Dec, 2020, 12:56: PM
Expert Answer
I guess the equation is
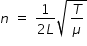................ (1)where n is frequency of transverse wave, L is length of string that forms stationary waves .
T is tension in the string and μ is linear mass density i.e., mass per unit length
Dimension of T = [ M L T -2 ]
Dimension of μ = [ M L-1 ]
Hence, dimension of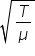 
= L T-1
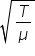= L T-1Dimension of RHS of eqn.(1) = L-1 L T -1 = T-1
In LHS of eqn.(1), we have frequency that hs dimension T -1
Hence dimension of LHS and RHS of eqn.(1) is matching exactly
Answered by Thiyagarajan K | 14 Dec, 2020, 12:38: AM
Concept Videos
-
Units and Measurement
This video explains significant figures, rules to identify significant figu... -
Units and Measurement
This video explains dimensions of physical quantities, dimensional formulae... -
Units and Measurement
This video contains practice questions on significant figures, dimensions a...
CBSE 11-science - Physics
Asked by derhebha955 | 03 Apr, 2024, 09:03: AM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by sumedhasingh238 | 28 Mar, 2024, 11:10: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by ss4172380 | 14 Nov, 2023, 08:05: AM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by doddisriman | 29 Oct, 2023, 09:43: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by Naveensharma2007 | 26 Jun, 2023, 06:54: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by manthansakhare050 | 18 Dec, 2022, 01:54: AM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by adibafatima2004 | 11 Sep, 2021, 08:02: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by suhani.pare | 28 Jun, 2021, 09:03: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by gopikagopakumar43 | 13 Dec, 2020, 12:56: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by sagarrc1564 | 11 Sep, 2020, 01:33: PM
ANSWERED BY EXPERT
