JEE Class main Answered

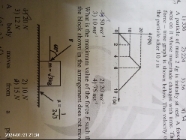
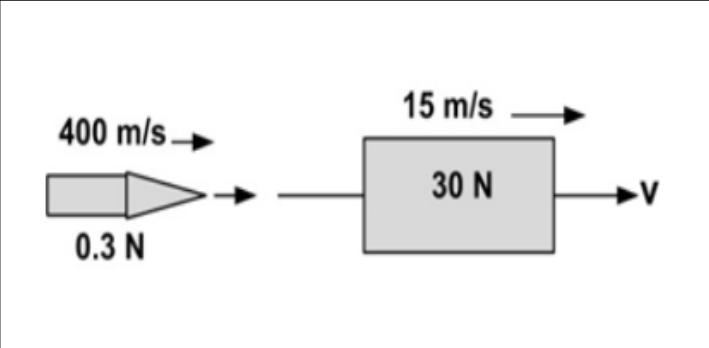
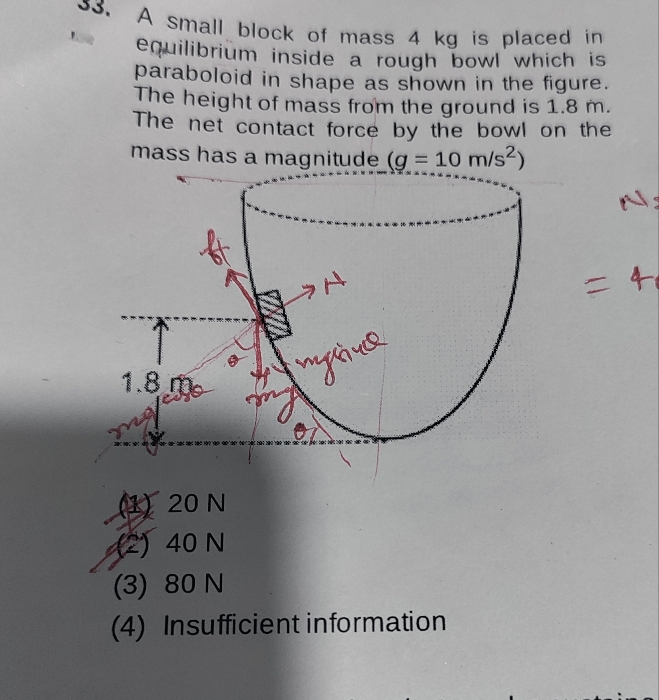
Please solve it

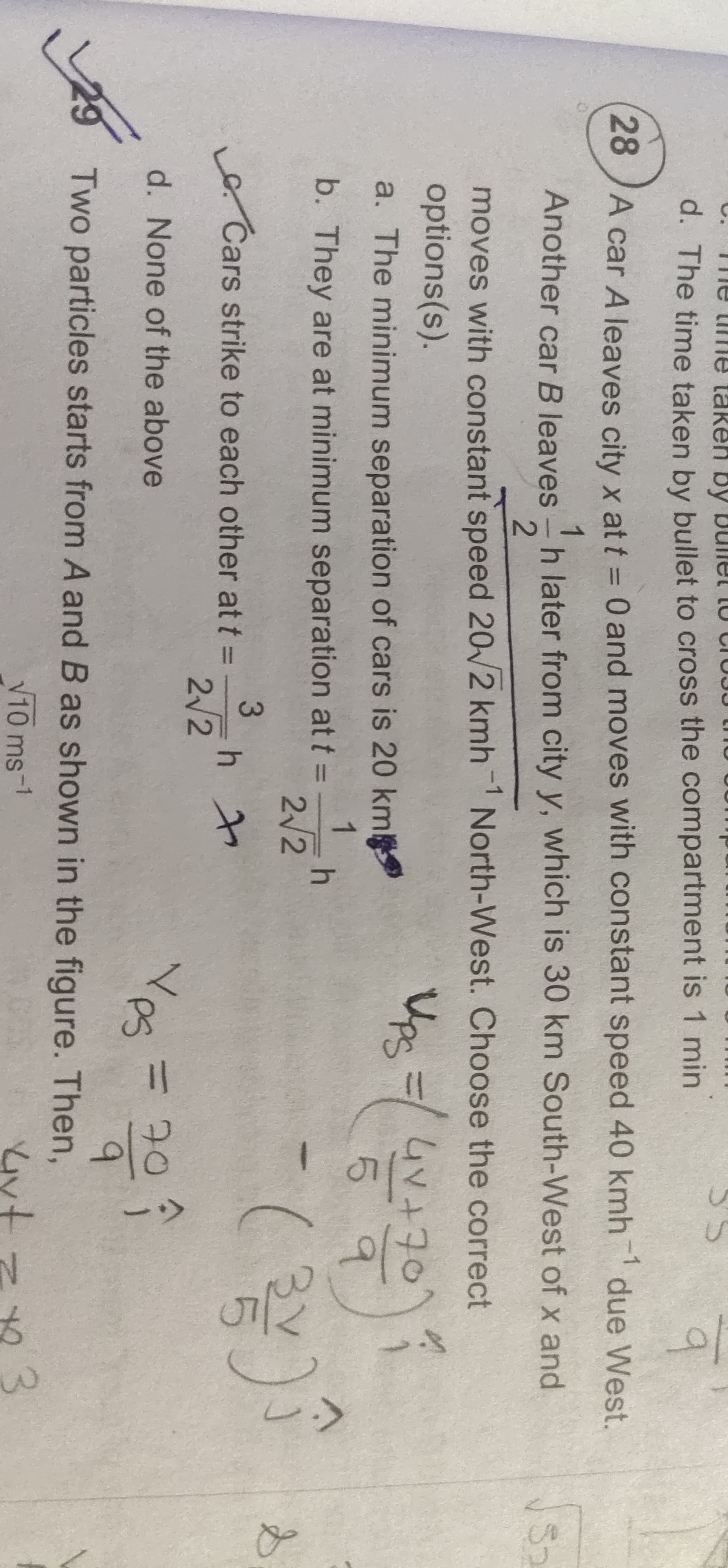
Asked by preetiagrawal1979 | 14 May, 2021, 06:43: AM

Expert Answer

Let city-x be the origin of cartesian coordinate system. Car-B starts half an hour after Car-A .

Let us assume our time t = 0 , when car-B starts to move.

Since car-A is moving at velocity 40 km/hr towards west , Coordinate of car-A at time t = 0 is given as

At t = 0 , coordinates of car-A = ( -40 × (1/2) km , 0 ) = ( -20 km, 0 )

Coordinate of car-A at time t = [ ( -20 - 40t ) km , 0 ] ..............................(1)

City-y is 30 km from city-x in the direction South-West

At t = 0 , coordinate of car-B = [ - ( 30 / √2 ) km , - ( 30 / √2 ) km ] = ( -21.213 km , -21.213 km )

Car-B is travelling with velocity 20√2 km/hr in north west direction .

Hence velocity components of car-B are given by

v_Bx = - 20 km/hr ; v_By = 20 km/hr

Coordinate of car-B at time t = [ - (21.213 + 20 t ) km , - (21.213 - 20 t ) km ] .......................... (2)

square of the distance S² between car-A and car-B at any time t is determined from

the coordinates given in (1) and (2) as follows

S² = { (1.213 -20t )² + ( 21.213 - 20t )² } ................................. (4)

To get the minimum distance between car-A and car-B , we differentiate above expression and

equate to zero to get the time t when the distance between the cars is minimum.

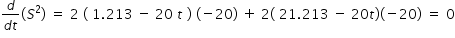
begin mathsize 14px style fraction numerator d over denominator d t end fraction open parentheses S squared close parentheses space equals space 2 space left parenthesis space 1.213 space minus space 20 space t space right parenthesis space left parenthesis negative 20 right parenthesis space plus space 2 left parenthesis space 21.213 space minus space 20 t right parenthesis left parenthesis negative 20 right parenthesis space equals space 0 end style

after simplification we get , t = 0.56 hour

Minimum distance S_min is determined from eqn.(4) by substituting t = 0.56 hour

we get, S_min = 14.14 km

-------------------------------------------------

Hence minimum distance between cars is not 20 km . Minimum distance is not at 1/(2√2) = 0.354 hour .

Cars will never strike at each other because we get S_min > 0

Answer to question :- (d) none of above

Answered by Thiyagarajan K | 14 May, 2021, 03:01: PM

Please Login or Sign up to continue!