A particle started moving in a straight line.Its acceleration at time t seconds is given by a=(-5t^(2)+5)m/s^(2) t>=0 .Find the time for its maximum velocity and maximum velocity of the particle v(max)?
Asked by sharadkumar12055
24th May 2021,
4:07 PM
Answered by Expert
Answer:
acceleration a =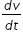 
= -5t2 + 5 ...................(1)
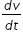= -5t2 + 5 ...................(1)maximum time t is determined by equating eqn.(1) to zero and solve for time t
-5t2 + 5 = 0
from above expression , we get , tmax = 1 s
Velocity as a function of time t is determined by integrating eqn.(1)
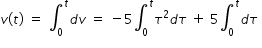
v(t) = -(5/3) t3 + 5 t
vmax is determined by substituting t =1 in above equation
vmax = -(5/3) + 5 = ( 10/3 ) m/s
Answered by Expert
24th May 2021,
5:04 PM
Rate this answer
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
You have rated this answer /10
Your answer has been posted successfully!
RELATED STUDY RESOURCES :
Browse free questions and answers by Chapters
- 1 Thermodynamics
- 2 Gravitation
- 3 Electromagnetic Waves
- 4 Communication Systems
- 5 Laws of Motion
- 6 Current Electricity
- 7 Work, Energy and Power
- 8 Kinematics
- 9 Physics and Measurement
- 10 Rotational Motion
- 11 Properties of Solids and Liquids
- 12 Kinetic Theory of Gases
- 13 Oscillations and Waves
- 14 Electrostatics
- 15 Magnetic Effects of Current and Magnetism
- 16 Electromagnetic Induction and Alternating Currents
- 17 Optics
- 18 Dual Nature of Matter and Radiation
- 19 Atoms and Nuclei
- 20 Electronic Devices
Trending Tags
Latest Questions
JEE Main Mathematics
Asked by amaladelsingh
28th October 2020,
10:24 PM
CBSE X Biology
Asked by reenacharan2008
28th October 2020,
9:11 PM
