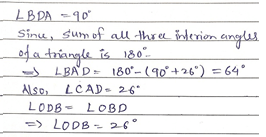Common Mistakes Made in ICSE Class 10 Board Exams - Chapter Circles

In this blog, we shall examine the world of circles, underlining the difficulties that frequently cause learners to give up. It tries to simplify the topic by pointing out and fixing the most prevalent mistakes made by students.

By Topperlearning Expert 21st Feb, 2024 | 11:00 am

Circles have gained a lot of attention from students as well as some great Mathematicians, because of its perfect symmetry and endless applications. Despite its simplicity, navigating through the details of circles can prove challenging for students.In this blog, we’ll delve into the most frequent mistakes made by students while attempting various questions based on circles. By identifying these errors and offering some insights to overcome the mistakes, we aim to encourage students to approach the questions based on circles with confidence and clarity. So, let’s first get clear with the concepts of circles and then delve into the common mistakes.

Overview of Circles:

A figure obtained by joining all those points in a plane which are at a constant distance from a fixed point in the same plane is called a circle.

The fixed point is called the centre of the circle.
Constant distance is called the radius.
The line segment joining any two points on the circumference of the circle is called a chord of the circle.
The longest chord or a chord passing through the centre of a circle is the diameter.

A line that touches a circle is a tangent to the circle and the point at which the line touches the circle is a point of contact. Moreover, the length of the tangent is the distance between the external point P and the point of contact with the circle.

One of the most important parts of a circle is a cyclic quadrilateral which is a quadrilateral inscribed in a circle.

There are a few theorems based on the circles which are listed below:

The angle which, an arc of a circle subtends at the centre is double that which it subtends at any point on the remaining part of the circumference.
Angles in the same segment of a circle are equal.
The angle in a semi-circle is a right angle.
The opposite angles of a cyclic quadrilateral are supplementary.
If a pair of opposite angles of a quadrilateral are supplementary, then the quadrilateral is cyclic.
The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.

For more details, click Revision notes on Circles.

Let’s now start discussing the mistakes made by students.

Mistake 1:

Not providing reasons supporting the answer

When any theorem is applied to conclude some statement or result, it is very important to state the reason for conclusion. But many students fail to do this as shown with an example below:

Example:

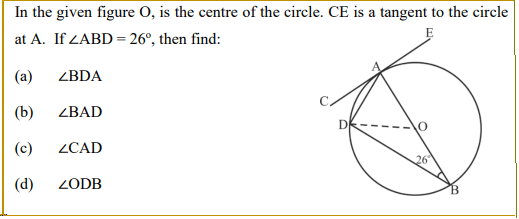
Solution(s) with mistake

Mistake 1_1

Reasons for taking, ∠BDA = 90°, ∠CAD = 26° and ∠ ODB = ∠OBD, are not mentioned.

Correct Solution

Mistake 1_2

To get one more example with proper reasoning, click “Example with reasons supporting the answer”.

Mistake 2:

Unable to use and apply the theorem correctly

It happens that the students do not apply the correct theorem or sometimes the theorem is correct but the execution does not go well. So, it is very important to recall the theorems when solving questions based on circles.

Such mistakes have been shown below with an example below:

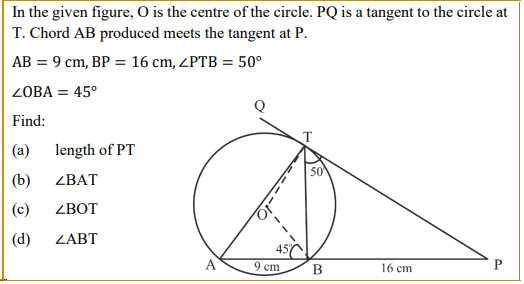
Solution(s) with mistake

Correct Solution

Mistake 2_1

Unable to apply the theorem for length of the tangent.

Mistake 2_2

Applied semi-circle theorem taking AT as the diameter which is incorrect.

Mistake 2_3

To view one such example with proper use of theorems, click “Example with appropriate theorems used”.

Mistake 3:

Misunderstanding the cyclic quadrilateral as any quadrilateral with its vertex (or vertices) inside the circle.

Many students consider any quadrilateral inside a circle as a cyclic quadrilateral, which is not correct and it may lead to the incorrect values of the different parts of the circle.

This is shown below with an example:

Example:

Solution with mistake

Correct Solution

Mistake 3_1

Cyclic quadrilateral is taken as ABCO instead of ABCD giving incorrect measure of ∠ABC.

Mistake 3_2

To explore one such example, click “Properties of Cyclic Quadrilateral”.

Mistake 4:

Measuring the lengths or angles of different parts of a figure given in the question paper using a ruler or compass

When it is asked to find the lengths or angles in a circle, many students measure the different parts of the actual figure (given in the question paper) which is not correct.

This is shown with an example below:

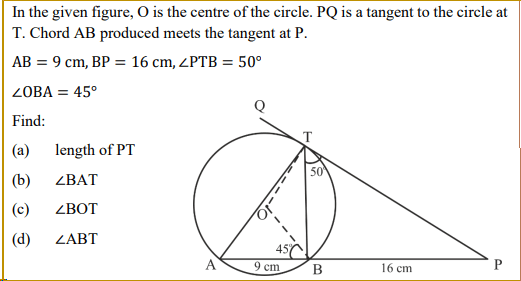
Solution with mistake

Mistake 4_1

Correct Solution

Mistake 4_2

Length of PT have been measured with ruler instead of calculating it.

To view one such example, click “Measuring the length with correct method”.

Conclusion:

In short, it is very important to be thorough with the concepts and properties of circles to achieve success in mathematics. In this blog, we discussed some most common mistakes made by students and the steps that must be taken to avoid these pitfalls when dealing with circles. The key ingredients to overcome these challenges are practice, patience and a willingness to learn from mistakes. With these, you can master the fascinating world circles. So, let's embrace these lessons, keep striving for improvement, and approach circles with confidence and clarity in our mathematical journey with the help of TopperLearning.

You can achieve all of these by accessing different resources like Multiple Choice Questions, Subjective Questions, Sample Papers, Assertion & Reasoning Questions, Revision Notes and Videos available for various boards like Maharashtra, CBSE and ICSE.