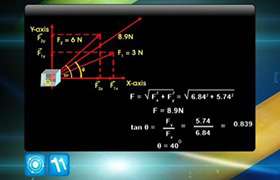
CBSE Class 11-science Answered
two vectors equal have resultant equal to either find the angle between them
Asked by choudharypriya65490 | 08 Sep, 2020, 12:26: AM
Let 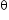 be the angle between the two vectors A and B such that, |A| = |B|.
be the angle between the two vectors A and B such that, |A| = |B|.
Therefore,
R2 = A2 + B2 + 2AB cos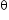
=> A2 = A2 + A2 + 2(A)(A) cos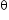 [since, |A| = |B| = |R|]
[since, |A| = |B| = |R|]
=> A2 = 2A2 + 2A2 cos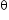
=> cos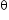 = -1/2
= -1/2
=> 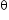 = 120°
= 120°
Answered by Shiwani Sawant | 08 Sep, 2020, 10:52: AM
Concept Videos
CBSE 11-science - Physics
Asked by vinitdubey7735 | 14 Mar, 2024, 11:21: AM
CBSE 11-science - Physics
Asked by dhanshreekansyakar | 09 Jan, 2024, 11:57: AM
CBSE 11-science - Physics
Asked by banhisikhapanda49 | 07 Nov, 2023, 10:42: PM
CBSE 11-science - Physics
Asked by preethiprithivi05 | 21 Feb, 2023, 09:28: PM
CBSE 11-science - Physics
Asked by rk274268 | 05 Aug, 2022, 01:19: PM
CBSE 11-science - Physics
Asked by Kattaithihaas | 24 Jul, 2022, 01:23: PM
CBSE 11-science - Physics
Asked by pawankumardas15492 | 22 Jul, 2022, 10:24: PM
CBSE 11-science - Physics
Asked by nutankumari95074 | 11 Jun, 2022, 05:24: PM
CBSE 11-science - Physics
Asked by kaziryan.05 | 13 Apr, 2022, 09:01: PM