Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

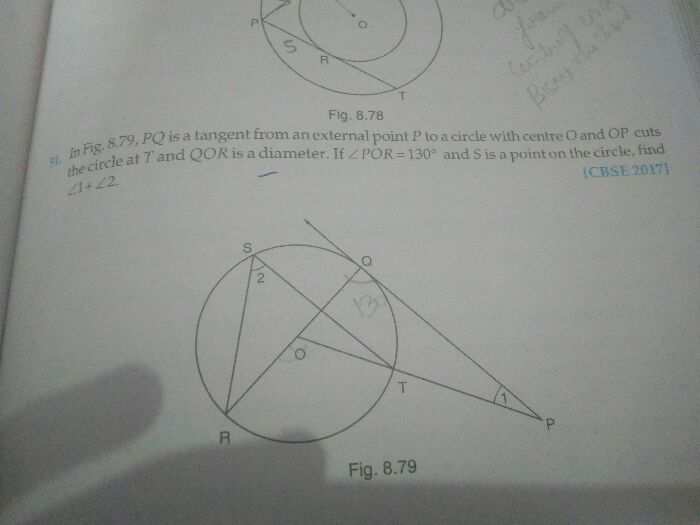
Two circles touches internally at a point P and from a point T ,the common tangent at P , tangent segments TQ and TR are drawn to the two circle Prove that TQ=TR
Asked by VasupradUboveja376 | 22 Jun, 2020, 00:03: AM
answered-by-expert Expert Answer
Question should be:
Two circles touches externally at a point P and from a point T, the common tangent at P, tangent segments TQ and TR are drawn to the two circle Prove that TQ=TR.
 
Proof:-
Let the circles be C1 and C2
C1 and C2 touch each other externally at P
From T, tangents are drawn
Tangent TQ on C1 and tangent TR on C2, common tangent is TP
Since, the tangents drawn from an external point are equal, we have
TP =TQ and TP = TR
Therefore, TQ = TR.
Answered by Renu Varma | 22 Jun, 2020, 11:33: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
PQ is a chord of length 8 cm to a circle of radius 5 cm. The tangents P and Q intersect at a point T. Find the length of the tangent TP.
Asked by yalagondanikhil | 16 Apr, 2024, 12:25: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
From a point P, two tangents PA and PB are drawn to a circle C(0, r).  If OP = 2r, then find ∠
Asked by riazu945 | 16 Jan, 2022, 13:00: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Q30
question image
Asked by sangyaswarupa | 16 Mar, 2021, 10:06: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
point A lies in the exterior of a circle with center P and radius 8 cm A tangent from A touches the circle at if AB=15 cm find PA
Asked by sinhkaran79 | 14 Mar, 2021, 12:59: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Question no.4 from the chapter Circles.
question image
Asked by s.saumya1011 | 05 Nov, 2020, 14:10: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
plz solve these
question image
Asked by brjkishorchauhan03 | 04 Nov, 2020, 12:10: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
question
question image
Asked by arindeep.singh | 02 Oct, 2020, 13:20: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
prove that a diameter AB of a circle bisects all those chords which are the tangent at the point A
Asked by shivappahb308 | 21 Sep, 2020, 14:15: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
question no 51
question image
Asked by vs4247325 | 04 Sep, 2020, 04:56: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Two circles touches internally at a point P and from a point T ,the common tangent at P , tangent segments TQ and TR are drawn to the two circle Prove that TQ=TR
Asked by VasupradUboveja376 | 22 Jun, 2020, 00:03: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt