CBSE Class 10 Answered
question no 51
Asked by vs4247325 | 04 Sep, 2020, 04:56: AM
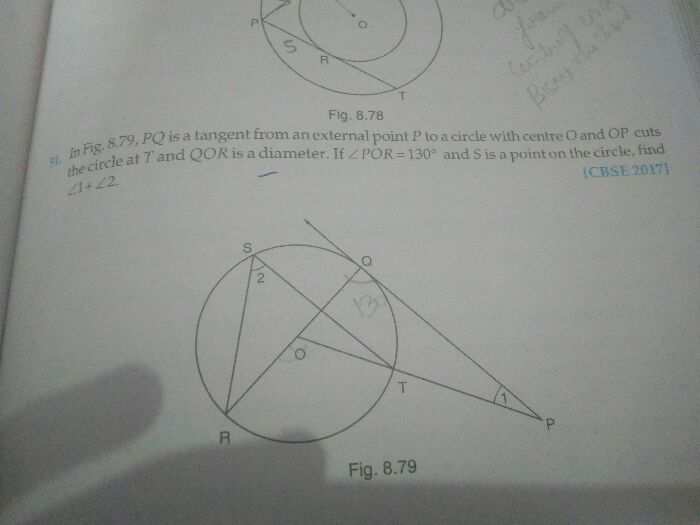
Question: In the figure, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and, QOR is a diameter. If ∠ POR = 130° and S is a point on the circle, find ∠ 1 + ∠ 2,
Given: ∠POR = 130° Given
∠POQ = 50° (since ∠POR and ∠POQ are supplementary)
∠PQO = 90° (∠ formed between the tangent and radius)
Consider triangle POQ, sum of all angles must be equal to 180°
∠POQ + ∠OPQ + ∠PQO = 180°
50° + ∠OPQ + 90° =180°
∠OPQ = 40°
∠OPQ = 1/2 ∠TOR ... (Angle made by an arc at centre is double the angle made by the same arc at any point on the circle)
∠OPQ = 1/2 ∠POR = 1/2 x 130° = 65°
∠2 = 65° and ∠1 = 40°
Hence, ∠2 + ∠1 = 105°
Answered by Renu Varma | 04 Sep, 2020, 01:26: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by yalagondanikhil | 16 Apr, 2024, 12:25: PM
CBSE 10 - Maths
Asked by riazu945 | 16 Jan, 2022, 01:00: PM
CBSE 10 - Maths
Asked by sinhkaran79 | 14 Mar, 2021, 12:59: PM
CBSE 10 - Maths
Asked by s.saumya1011 | 05 Nov, 2020, 02:10: PM
CBSE 10 - Maths
Asked by brjkishorchauhan03 | 04 Nov, 2020, 12:10: PM
CBSE 10 - Maths
Asked by shivappahb308 | 21 Sep, 2020, 02:15: PM
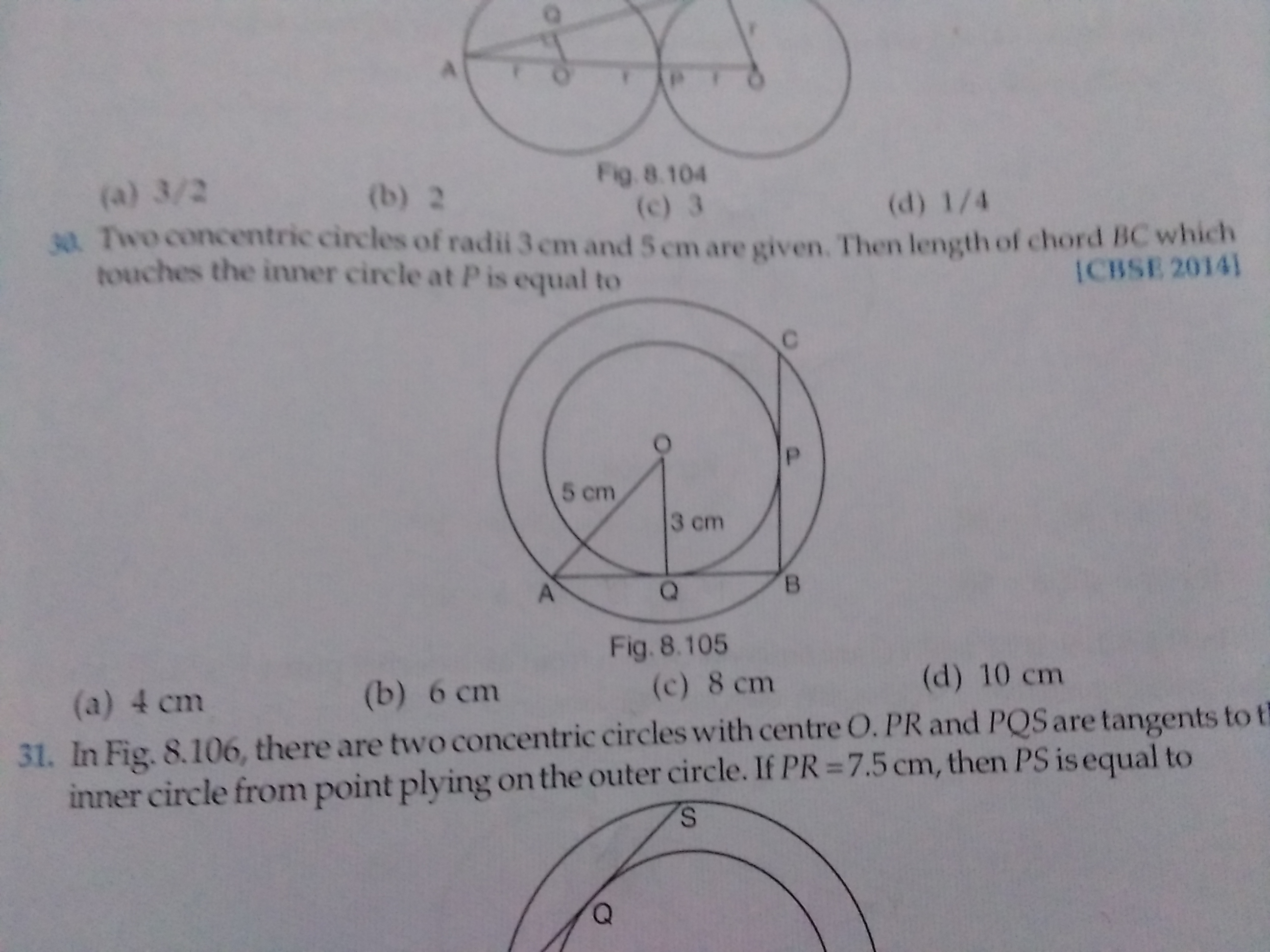
CBSE 10 - Maths
Asked by VasupradUboveja376 | 22 Jun, 2020, 12:03: AM