Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

question
question image
Asked by arindeep.singh | 02 Oct, 2020, 13:20: PM
answered-by-expert Expert Answer
Question:
 
Solution:

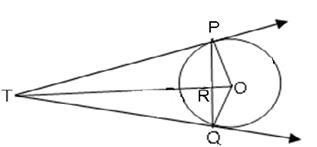
Let TR = y

Since OT is perpendicular bisector of PQ.

Therefore, PR=QR=4cm

In right triangle OTP and PTR, we have,

TP2 = TR2 + PR2

Also, OT2 = TP2 + OP2

OT2 = (TR2+PR2) + OP2

(y+3)2 = y2 + 16 + 25  ... (OR = 3, as OR2 = OP2 - PR2)

 

6y=32

 y=

TP2=TR2+PR2

TP2=+42 = +16 = 

TP=  cm

Let TR = y

Since OT

is perpendicular bisector of PQ.

Therefore, PR=QR=4cm

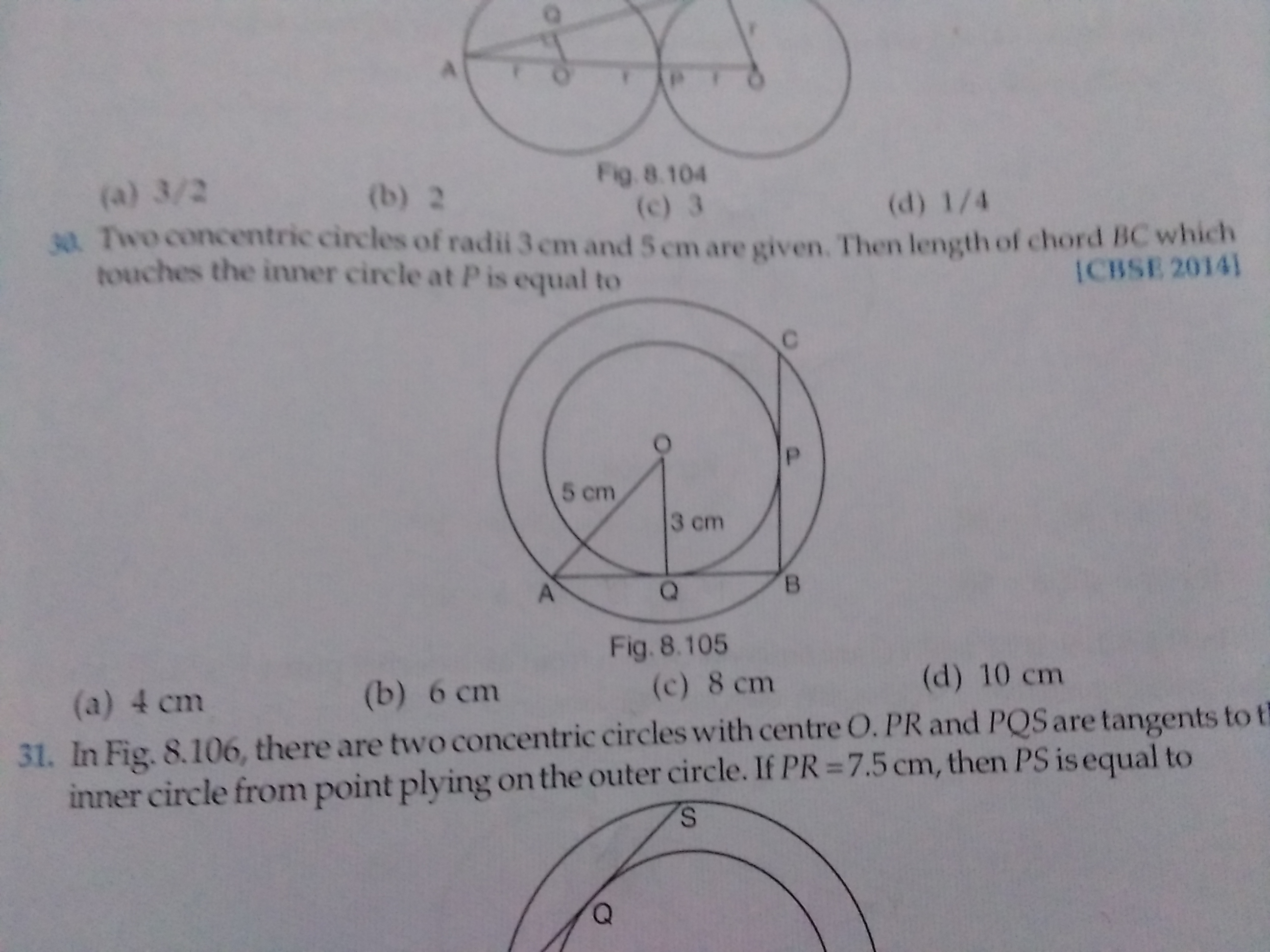
In right triangle OTP and PTR, we have,

TP2=TR2+PR2

Also, OT2=TP2+OP2

OT2=(TR2+PR2) + OP2

(y+3)2=y2+16+25 (OR = 3, as OR2 = OP2 - PR2)

Answered by Renu Varma | 03 Oct, 2020, 16:08: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
PQ is a chord of length 8 cm to a circle of radius 5 cm. The tangents P and Q intersect at a point T. Find the length of the tangent TP.
Asked by yalagondanikhil | 16 Apr, 2024, 12:25: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
From a point P, two tangents PA and PB are drawn to a circle C(0, r).  If OP = 2r, then find ∠
Asked by riazu945 | 16 Jan, 2022, 13:00: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Q30
question image
Asked by sangyaswarupa | 16 Mar, 2021, 10:06: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
point A lies in the exterior of a circle with center P and radius 8 cm A tangent from A touches the circle at if AB=15 cm find PA
Asked by sinhkaran79 | 14 Mar, 2021, 12:59: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Question no.4 from the chapter Circles.
question image
Asked by s.saumya1011 | 05 Nov, 2020, 14:10: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
plz solve these
question image
Asked by brjkishorchauhan03 | 04 Nov, 2020, 12:10: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
question
question image
Asked by arindeep.singh | 02 Oct, 2020, 13:20: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
prove that a diameter AB of a circle bisects all those chords which are the tangent at the point A
Asked by shivappahb308 | 21 Sep, 2020, 14:15: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
question no 51
question image
Asked by vs4247325 | 04 Sep, 2020, 04:56: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Two circles touches internally at a point P and from a point T ,the common tangent at P , tangent segments TQ and TR are drawn to the two circle Prove that TQ=TR
Asked by VasupradUboveja376 | 22 Jun, 2020, 00:03: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt