CBSE Class 12-science Answered
Area of the plates of a parallel plate capacitor, A = 90 cm2 = 90 x 10-4m2 Distance between the plates, d = 2.5 mm = 2.5 x 10-3 m potential difference across the plates, V = 400 V
- Capacitance of the capacitor is given by the relation,
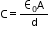
Electrostatic energy stored in the capacitor is given by the relation, 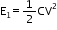
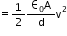
Where,
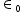 = Permittivity of free space = 8.85 x 10-12C2N-1m-2
= Permittivity of free space = 8.85 x 10-12C2N-1m-2
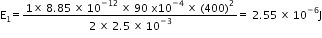
Hence, the electrostatic energy stored by the capacitor is 2.55 x 10-6J
(b) Volume of the given capacitor,
V' = A x d
= 90 x 10-4 x 2.5 x 10-3
= 2.25 x 10-5 m3
Energy stored in the capacitor per unit volume is given by,
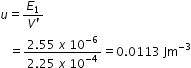
Again, 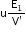

Where,
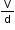 = Electric intensity = E
= Electric intensity = E
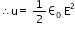
(c) When zero of potential energy is taken, d1=1.06 
Therefore, Potential energy of the system = Potential energy at d1 - Potential energy at d

= 21.73 x 10-19J - 27.2eV
= 13.58eV - 27.2eV
= -13.6eV




 . In the ground state of an
. In the ground state of an 