CBSE Class 12-science Answered
If one of the two electrons of a H2 molecule is removed, we get a hydrogen molecular ion 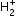 . In the ground state of an
. In the ground state of an 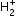 , the two protons are separated by roughly 1.5
, the two protons are separated by roughly 1.5 , and the electron is roughly 1
, and the electron is roughly 1 from each proton. Determine the potential energy of the system. Specify your choice of the zero of potential energy.
from each proton. Determine the potential energy of the system. Specify your choice of the zero of potential energy.
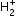 . In the ground state of an
. In the ground state of an 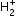 , the two protons are separated by roughly 1.5
, the two protons are separated by roughly 1.5 , and the electron is roughly 1
, and the electron is roughly 1 from each proton. Determine the potential energy of the system. Specify your choice of the zero of potential energy.
from each proton. Determine the potential energy of the system. Specify your choice of the zero of potential energy.
Asked by Topperlearning User | 22 Apr, 2015, 07:50: AM
The system of two protons and one electron is represented in the given figure.
Charge on proton 1, q1 = 1.6 x 10-19 C
Charge on proton 2, q2 = 1.6 x 10-19 C
Charge on electron, q3 = -1.6 x 10-19 C
Distance between protons 1 and 2, d1 = 1.5 x 10-10 m
Distance between proton 1 and electron, d2 = 1 x 10-10 m
Distance between proton 2 and electron, d3 = 1 x 10-10 m
The potential energy at infinity is zero.
potential energy of the system,
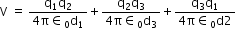
Substituting 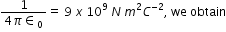
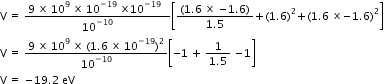
Therefore, the potential energy of the system is - 19.2 eV.
Answered by | 22 Apr, 2015, 09:50: AM
Concept Videos
CBSE 12-science - Physics
Asked by dasrituparna1999 | 13 Apr, 2024, 06:56: AM
CBSE 12-science - Physics
Asked by sankaraganapathy007 | 09 Sep, 2023, 22:03: PM
CBSE 12-science - Physics
Asked by tahseenaamir07 | 25 Jun, 2022, 01:33: AM
CBSE 12-science - Physics
Asked by sindhusoman87 | 15 Jul, 2020, 08:33: AM
CBSE 12-science - Physics
Asked by Shankaramurthy064 | 13 May, 2020, 08:47: AM
CBSE 12-science - Physics
Asked by Topperlearning User | 22 Apr, 2015, 07:50: AM
CBSE 12-science - Physics
Asked by Topperlearning User | 22 Apr, 2015, 09:59: AM
CBSE 12-science - Physics
Asked by Topperlearning User | 22 Apr, 2015, 08:40: AM
CBSE 12-science - Physics
Asked by Topperlearning User | 23 Apr, 2015, 11:40: AM
CBSE 12-science - Physics
Asked by Topperlearning User | 24 Apr, 2015, 14:08: PM




 . In the ground state of an
. In the ground state of an 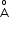 , and the electron is roughly 1
, and the electron is roughly 1