CBSE Class 11-science Answered

the moment of inertia of semicircular ring about an axis which is perpendicular to the plane of the ring and passes through centre

Asked by raghuwanshidaksh9 | 14 Oct, 2019, 17:48: PM

Expert Answer

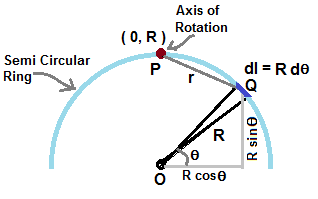
Figure shows a semi-circular ring of radius R.

Let the centre of curvature O coincides with origin of polar coordinate (r-θ) system .

It is required to get moment of inertia about axis passing through P which is the geometrical centre of semi-circular ring.

Axis of rotation is perpendicular to the plane of ring.

Let us consider a small length dl of ring at Q . If the line joining Q to origin makes angle θ with reference line

and length dl subtends angle dθ, then this small length equals ( R dθ).

If M is mass of whole ring and mass is uniformly distributed, mass density m, i.e. mass per unit length is given by , m = M/(πR)

If Polar coordinates of point Q is (Rcosθ , Rsinθ) and that of point P (0,R) then distance PQ is given by,

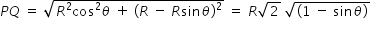
begin mathsize 14px style P Q space equals space square root of R squared cos squared theta space plus space open parentheses R space minus space R sin theta close parentheses squared end root space equals space R square root of 2 space square root of open parentheses 1 space minus space sin theta close parentheses end root end style

Moment of inertia of small length at Q, dI = dm r² .............(1)

where dm is mass of small length, m×dl = m×R dθ ...................(2)

Hence moment of inertia I of whole ring is given by,

begin mathsize 14px style I space equals space integral d I space equals space m space 2 R cubed integral subscript 0 superscript pi left parenthesis 1 minus sin theta right parenthesis d theta space equals space m space 2 R cubed space open parentheses pi space minus space 2 close parentheses space equals space open parentheses fraction numerator M over denominator pi R end fraction close parentheses space 2 R cubed space open parentheses pi space minus space 2 close parentheses space equals space fraction numerator 2 open parentheses pi minus 2 close parentheses over denominator pi end fraction M R squared end style

I = 0.363 M R²

Answered by Thiyagarajan K | 15 Oct, 2019, 09:22: AM

Concept Videos