CBSE Class 9 Answered
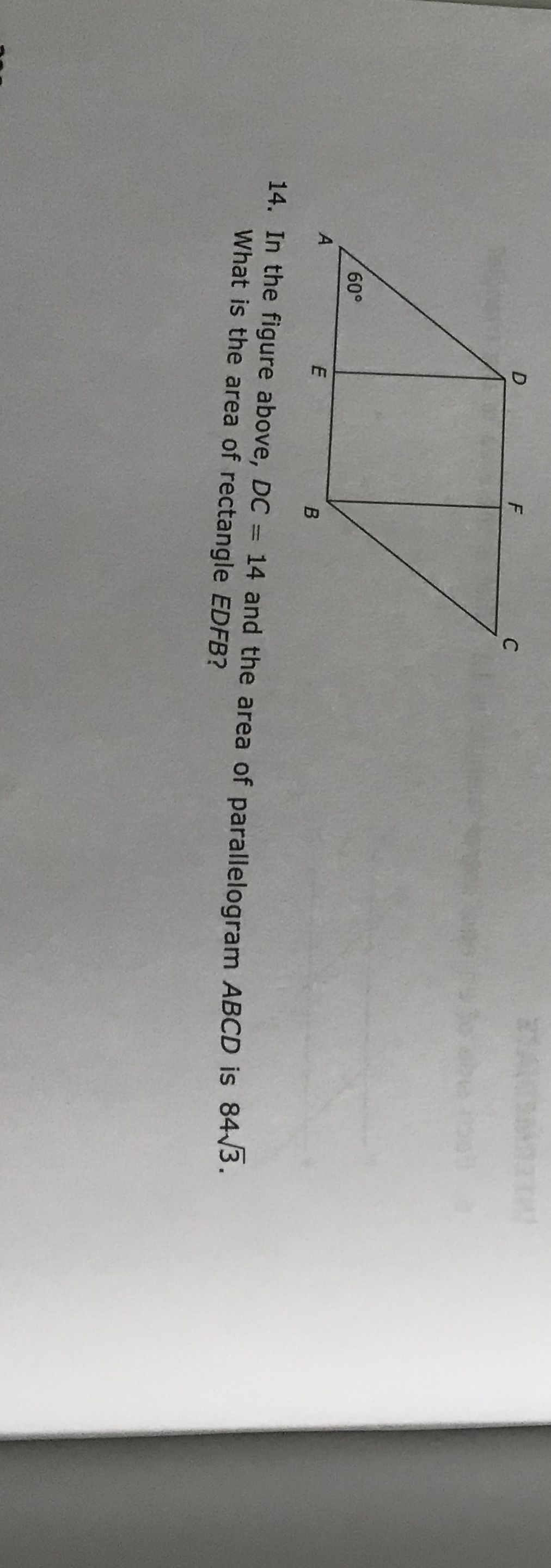
The figure shows two parallelograms ABCD and ABEF. Prove that Area of 
ADF = area of BCE.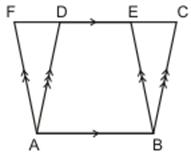
Asked by Topperlearning User | 17 Aug, 2017, 01:59: PM
Expert Answer
Parallelogram ABCD and parallelogram ABEF are on the same base AB and between the same parallels AB and FC.
ar (ABCD) = ar (ABEF)Now ar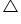 
(ADF) = 
ar (ABEF)
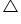(ADF) = ar (ABEF) (Same base AB and between the same parallels AB and FE)
Similarly, ar 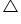(BCE) =
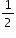ar (ABCD)
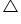(BCE) =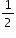ar (ABCD)
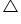ar (ADF) = ar 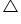(BCE)
Answered by | 17 Aug, 2017, 03:59: PM
Application Videos
-
This video explains a case study question which make use of the formula ...
-
This video explains a case study question where a triangle and a paralle...
-
This video explains a case study question where a triangle and a paralle...
-
This video explains a case study question where a triangle and a paralle...
CBSE 9 - Maths
Asked by yadavPriy000 | 06 May, 2021, 07:11: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by maddinenianr | 21 Mar, 2020, 03:48: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by prakash.sanyasi | 04 Jan, 2020, 05:09: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by suresh | 27 Nov, 2019, 09:21: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by shrivastavaabhi727 | 12 Sep, 2019, 07:53: PM
ANSWERED BY EXPERT
CBSE 9 - Maths
Asked by vikasg13.hardware | 23 Jun, 2018, 05:32: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by Topperlearning User | 17 Aug, 2017, 01:50: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by Topperlearning User | 17 Aug, 2017, 01:59: PM
ANSWERED BY EXPERTCBSE 9 - Maths
ABC. 
Asked by Topperlearning User | 17 Aug, 2017, 01:56: PM
ANSWERED BY EXPERT