CBSE Class 9 Answered
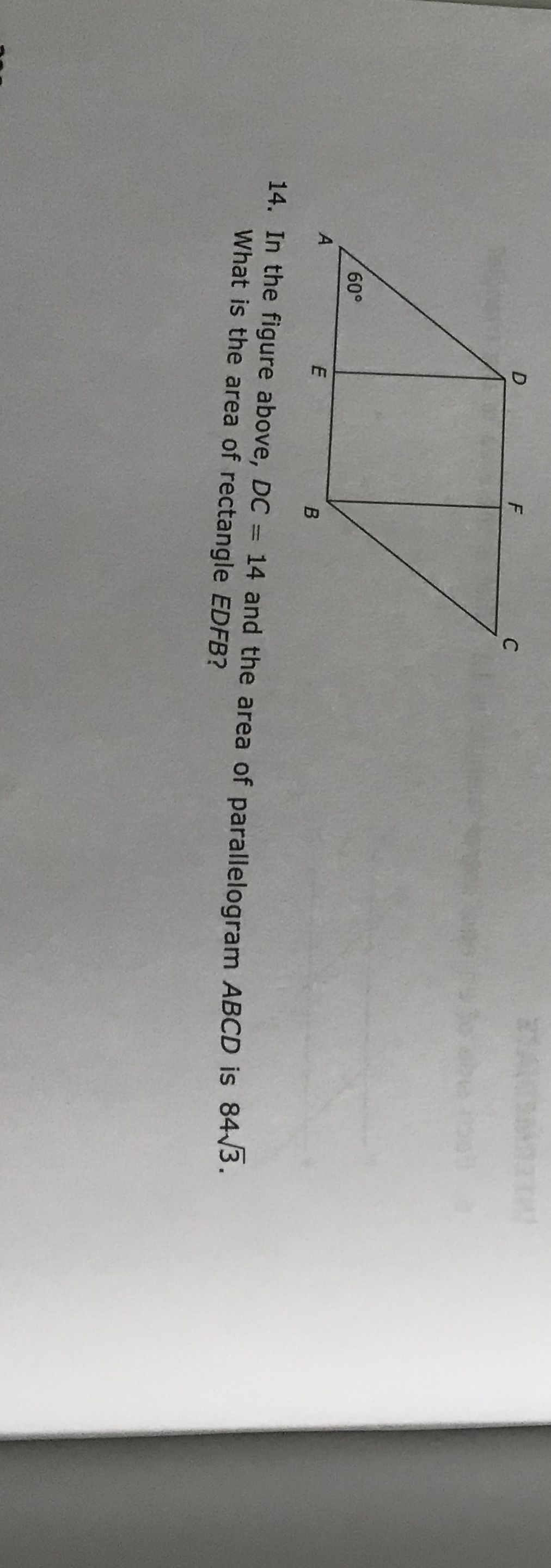
The diagonals of a parallelogram ABCD intersect at point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area that is ar (APQB) = ar (PQCD). 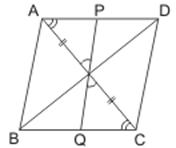

Asked by Topperlearning User | 17 Aug, 2017, 01:53: PM
Diagonals of a parallelogram divide it into two triangles of equal area.
From (i) and (ii)
ar (ABQO) + ar (COQ) = ar (CDPO) + ar (AOP)
Answered by | 17 Aug, 2017, 03:53: PM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by yadavPriy000 | 06 May, 2021, 07:11: PM
CBSE 9 - Maths
Asked by maddinenianr | 21 Mar, 2020, 03:48: PM
CBSE 9 - Maths
Asked by prakash.sanyasi | 04 Jan, 2020, 05:09: PM
CBSE 9 - Maths
Asked by suresh | 27 Nov, 2019, 09:21: PM
CBSE 9 - Maths
Asked by shrivastavaabhi727 | 12 Sep, 2019, 07:53: PM
CBSE 9 - Maths
Asked by vikasg13.hardware | 23 Jun, 2018, 05:32: PM
CBSE 9 - Maths
Asked by Topperlearning User | 17 Aug, 2017, 01:50: PM
CBSE 9 - Maths
Asked by Topperlearning User | 17 Aug, 2017, 01:59: PM
CBSE 9 - Maths
Asked by Topperlearning User | 17 Aug, 2017, 01:56: PM