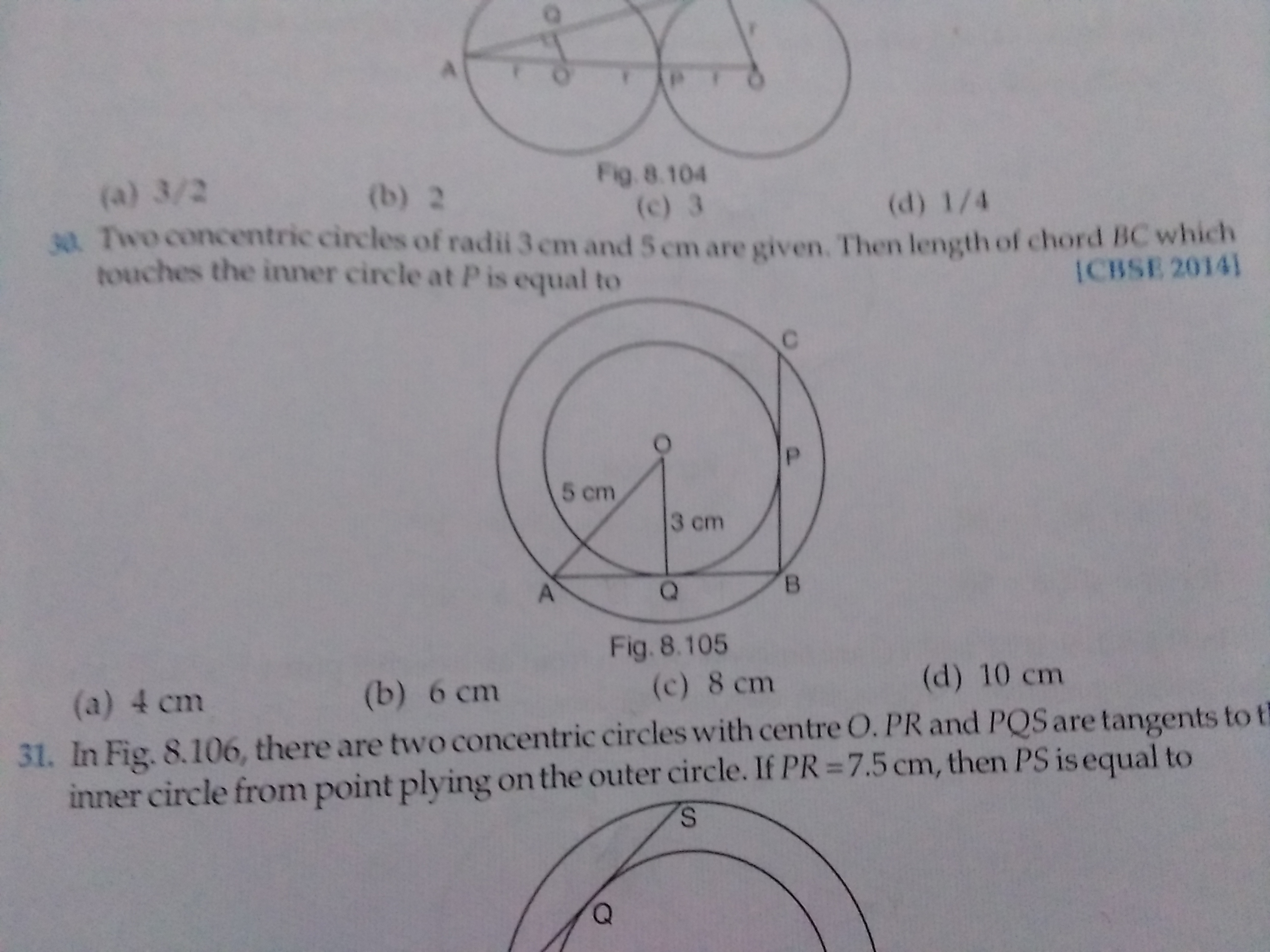
CBSE Class 10 Answered

Since, OT is perpendicular bisector of PQ, therefore
PR = RQ… (1)
ButPQ = 8 km (given)
![]() PR + RQ = 8
PR + RQ = 8
![]() PR + PR= 8[using (1)]
PR + PR= 8[using (1)]
![]() PR = 4
PR = 4
![]() RQ = PR = 4 km... (2) [using (1)]
RQ = PR = 4 km... (2) [using (1)]
In right triangle ORP, we have:
OP2 = OR2 + PR2
![]() OR2 = OP2 - PR2
OR2 = OP2 - PR2
![]() OR2 = 25 - 16 = 9
OR2 = 25 - 16 = 9
![]() OR = 3 km
OR = 3 km
Since, TP is tangent to circle with centre O and OP is its radius, therefore,
OP ![]() TP
TP
[![]() The tangent at any point of a circle is perpendicular to the radius through the point of contact]
The tangent at any point of a circle is perpendicular to the radius through the point of contact]
![]()
![]() OPT = 90o
OPT = 90o
In right triangle OPT, we have:
OT2 = PT2 + OP2
![]() (TR + OR)2 = PT2 + 25
(TR + OR)2 = PT2 + 25
![]() (TR + 3)2 = PT2 + 25... (4)
(TR + 3)2 = PT2 + 25... (4)
In right triangle PRT, we have:
PT2 = TR2 + PR2
![]() PT2 = TR2 + 16... (5) [using (2)]
PT2 = TR2 + 16... (5) [using (2)]
From(4) and (5), we have:
(TR + 3)2 = (TR2 + 16) + 25
![]() TR2 + 9 + 6TR = TR2 + 41
TR2 + 9 + 6TR = TR2 + 41
![]() 6TR = 32
6TR = 32
![]() TR =
TR = ![]() ... (6)
... (6)
Now, from (5) and (6), we get
![]()
![]()
![]()
![]()
![]()
We know tangents drawn from an external point to a circle are equal in length.
So, TP = TQ
![]() Total length of the roads TP and TQ =
Total length of the roads TP and TQ = ![]() km
km
Total cost of roads = ![]() = Rs. 1,60000
= Rs. 1,60000
The contractors, concerned engineers and officers should be honest and persons of integrity and strong character. There should be no political interference and demands except honesty and fair control on the quality of construction. Then the country will shine.