CBSE Class 12-science Answered
Please refer to the uploaded image for the doubt
Asked by arjunsah797 | 14 May, 2022, 01:34: PM
Expert Answer
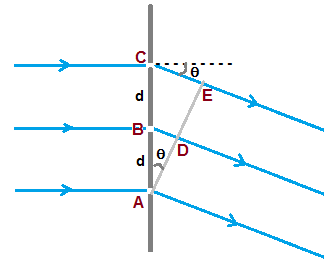
Part (a) (i)
Path difference between A and D = d sinθ
Phase difference between A and D = ( 2π / λ ) ( d sinθ )
where d is distance between slits , λ is wave length of light.
----------------------------------------
Part (a) (ii)
Path length ΔS between C and E, ΔS = 2d sinθ
In order to get constructive interference between light rays emerging from C and A
ΔS = 2d sinθ = nλ
where n is an positive integer ( n>0 )
In order to get destructive interference between light rays emerging from C and A
ΔS = 2d sinθ = (2n+1) ( λ / 2 )
-----------------------------------------------------------------
Part (a) (iii )
For constructive interference, path length ΔS between light rays emerging from successive slits
ΔS = d sinθ = nλ
For second order diffraction n = 2
hence we get , 2 λ = d sinθ
---------------------------------------------------
Part (b)
sine of angle of diffraction is given as
sinθ = n ( λ / d )
wavelength of light λ = 486 nm
distance between slits = 1/ N = 1 / ( 4.5 × 105 ) = 2.222 × 10-6
where N is number of lines per metre in the grating
sinθ = n ( λ / d ) = n ( 486 × 10-9 ) / ( 2.222 × 10-6 ) = 0.219 n
sinθ should be ≤ 1
Hence maximum value of n = 4
Maximum order of diffraction is 4
-----------------------------------------------------------
Part (c)
whilte light consists of light rays of different wavelength ranging from 400 nm to 700 nm .
Hence different wavelengths have diffraction maxima at different angles.
In the diffraction pattern, we see maxima of different wavelengths at different points .
Hence we see rainbow of colors ranging from violet to red
Answered by Thiyagarajan K | 14 May, 2022, 04:40: PM
CBSE 12-science - Physics
Asked by suman.sh01 | 21 May, 2022, 11:09: AM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by arjunsah797 | 14 May, 2022, 01:34: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by sirib942254 | 04 Aug, 2021, 08:30: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by ramdasiyogesh2001 | 12 Mar, 2021, 12:47: AM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by dsdeepak487 | 27 Feb, 2020, 06:06: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by Abhineet | 26 Nov, 2019, 02:04: AM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by Abhineet | 26 Nov, 2019, 02:03: AM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by vanshrathod71 | 30 Jan, 2019, 12:38: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by Topperlearning User | 13 Jun, 2014, 07:29: AM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by Topperlearning User | 13 Jun, 2014, 07:39: AM
ANSWERED BY EXPERT