CBSE Class 9 Answered
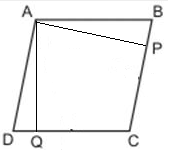
In Parallelogram ABCD o is any point on the diagonal bd .prove that area of triangle OAB=area of triangle COB
Asked by Muruga | 17 Jan, 2018, 04:43: PM
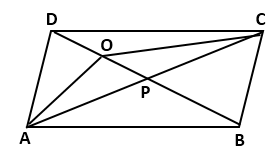

Answered by Rashmi Khot | 18 Jan, 2018, 10:27: AM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by yadavPriy000 | 06 May, 2021, 07:11: PM
CBSE 9 - Maths
Asked by maddinenianr | 21 Mar, 2020, 03:48: PM
CBSE 9 - Maths
Asked by prakash.sanyasi | 04 Jan, 2020, 05:09: PM
CBSE 9 - Maths
Asked by suresh | 27 Nov, 2019, 09:21: PM
CBSE 9 - Maths
Asked by shrivastavaabhi727 | 12 Sep, 2019, 07:53: PM
CBSE 9 - Maths
Asked by vikasg13.hardware | 23 Jun, 2018, 05:32: PM
CBSE 9 - Maths
Asked by Topperlearning User | 17 Aug, 2017, 01:50: PM
CBSE 9 - Maths
Asked by Topperlearning User | 17 Aug, 2017, 01:59: PM
CBSE 9 - Maths
Asked by Topperlearning User | 17 Aug, 2017, 01:56: PM