Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

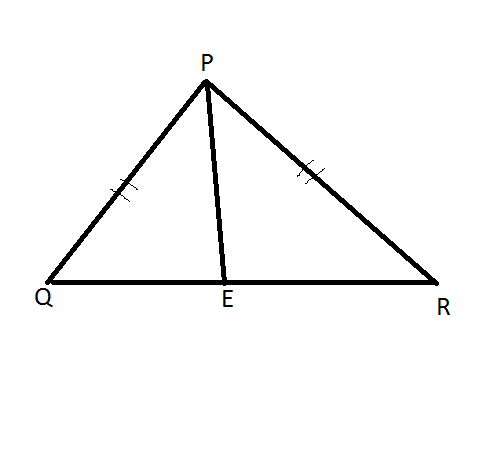
In a triangle PQR,
PQ=PR and the lengths of the sides are integers.
E is the midpoint of QR.
QE,PE and PQ are in arithmetic progression.
Then what is the least possible value of perimeter of the triangle PQR?
 
Asked by Susan fletcher | 26 May, 2014, 11:06: AM
answered-by-expert Expert Answer
G i v e n comma space Q E comma space P E comma space P Q space a r e space i n space A P space w h i c h space m e a n s P E equals fraction numerator Q E plus P Q over denominator 2 end fraction Q E equals fraction numerator Q R over denominator 2 end fraction S o comma space 2 P E space equals space fraction numerator Q R over denominator 2 end fraction plus P Q 4 P E equals space 2 P Q plus Q R ; P e r i m e t e r space o f space t r a i n g l e space P Q R space i s space P Q space plus thin space Q R space plus thin space P R b u t space g i v e n space P Q space equals space P R S o space p e r i m e t e r space b e c o m e s space 2 P Q space plus thin space Q R f r o m space a b o v e space e q u a t i o n space w e space h a v e space 2 P Q space plus thin space Q R space equals space 4 space P E S o space m i n i m u m space v a l u e space o f space p e r i m e t e r space i s space 4 space P E space w h i c h space i s space 4 space t i m e s space m e d i a n. space
Answered by Dharma Teja | 04 Jun, 2014, 03:27: PM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 12-science - Maths
question no 24
question image
Asked by shubh31122006 | 01 Feb, 2024, 09:06: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
solve it
question image
Asked by sdmbotch1123 | 23 Sep, 2023, 06:51: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Distance between two parallel planes 2x+y+2z=9 and 4x+2y+4z+5=0    
Asked by kishanradha7392 | 05 Jul, 2022, 04:26: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Two lines given- L₁: x+1/3 = y-3/-2 = z+2/-1 L₂: x/-1=y-7/3=z+7/-2 Find the point of intersection of the lines L₁ and L₂.
Asked by suman.sh01 | 07 Jun, 2022, 07:22: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find the angle between two lines whose directions cosines are given by l+m+n=0 and l^2+m^2-n^2=0.[**WITHOUT USING THEOREMS OF VECTOR**]
Asked by arjunsah797 | 02 May, 2022, 09:30: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Distance of a point 1,0,-3 from the planex-y-z measured parllel to the line x-2/2=y+2/3=z-6/-6
Asked by Madhureddymamilla | 06 Jan, 2020, 01:11: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Pl ans
question image
Asked by jain.pradeep | 03 Dec, 2019, 06:18: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
The value of direction cosine of two straight lines can satisfy the two equation, 3l+m+5n=0 & 6mn-2nl+5lm=0 . Find the angle between those lines.  
Asked by rsjkumar2003 | 23 Sep, 2019, 01:09: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
prove that vectors -2i -2j+4k , -2i+4j -2k , 4i -2j -2k are coplanar ?
Asked by harshgarg18012003 | 26 Jun, 2019, 09:11: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
A vertical line  l passes through the point (2,3). A horizontal line m passes through the point (-1,6). At what coordinate points do l and m intersect?
Asked by tv2000in | 25 May, 2019, 06:25: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×