CBSE Class 12-science - Equation of Plane Videos
Equation of a Plane
This video explains the equation of a plane in normal form, perpendicular to a given vector and passing through a given point.
More videos from this chapter
View All-
Introduction to 3D Geometry
-
Introduction to 3D Geometry
-
Introduction to 3D Geometry
-
Cartesian equation of a line
-
Cartesian equation of a line
-
Q 48
-
If
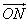is the normal from the origin to the plane, and 
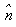is the unit vector along 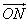. P(x, y, z) be any point on the plane and 
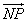is perpendicular to 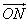. Find the equation of plane in the normal form.
-
Let
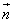be the vector normal to the plane and 
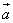be the position vector of the point through which the plane passes. Then find the equation of plane.
-
Find the equation of the plane, which is at a distance of 5 unit from the origin and has
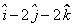as a normal vector.
- Find the equation of the plane whose distance from the origin is 8 units and the direction ratios of the normal are 6, – 3, – 2.
-
Find the equation of the plane is
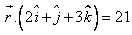. Find the perpendicular distance of the plane from the origin.
-
Write the normal and Cartesian form of the plane
.
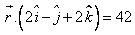- Find the equation of the plane passing through the points (–1, 4, – 3), (3, 2, – 5) and (– 3, 8, – 5).
- Find the equation of the plane passing through the point (3, – 3, 1) and perpendicular to the line joining the points (3, 4, – 1) and (2, – 1, 5).
- Find the co-ordinates of the foot of the perpendicular drawn from the origin to the plane 2x – 3y + 6z + 7 = 0.
