CBSE Class 12-science Answered
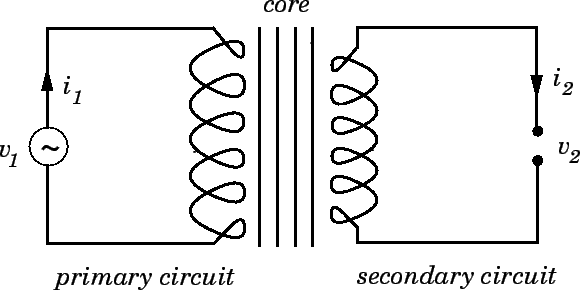
Let us consider a particularly simple transformer in which the primary and secondary coils are solenoids sharing the same air-filled core. Suppose that ![]() is the length of the core, and
is the length of the core, and ![]() is its cross-sectional area. Let
is its cross-sectional area. Let ![]() be the total number of turns in the primary coil, and let
be the total number of turns in the primary coil, and let ![]() be the total number of turns in the secondary coil. Suppose that an alternating voltage
be the total number of turns in the secondary coil. Suppose that an alternating voltage
where
in the secondary circuit, where
around the secondary circuit, where
The circuit equation for the primary circuit is written
assuming that there is negligible resistance in this circuit. The first term in the above equation is the externally generated emf. The second term is the back-emf due to the self inductancesince
The alternating emf generated in the secondary circuit consists of the emf generated by the self inductance ![]() of the secondary coil, plus the emf generated by the mutual inductance of the primary and secondary coils. Thus,
of the secondary coil, plus the emf generated by the mutual inductance of the primary and secondary coils. Thus,
Now, the instantaneous power output of the external AC power source which drives the primary circuit is
| (290) |
| (291) |
| (292) |
Equations 286,289 and 293 yield
| (294) |
| (295) |
Equations 293 and 296 can be combined to give
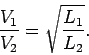 |
(297) |
the self inductances of the primary and secondary coils are given by ![]() and
and ![]() , respectively. It follows that
, respectively. It follows that
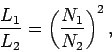 |
(298) |