CBSE Class 10 Answered

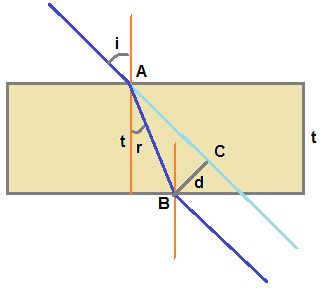
Lateral displacement is the perpendicular distance between incident ray and emergent ray , when light ray is refracted through transparent slab as shown in figure.

In figure lateral displacement is BC = d .

From right ΔABC we knaoe d = AB sin(i-r)

AB = t / cos (r)

where i is angle of incidence, r is angle of refraction and t is thickness of slab

Hence lateral displacement  d = [ t sin (i-r) ] / cos (r)   ..........................(1)

In special case where angle of incidence i and angle of refraction are small

sin( i - r ) ≈ ( i - r )   and cos (r) ≈ 1

Hence , we rewrite eqn.91) as  d = t ( i - r )  ........................(2)

By law of refraction = sin(i) / sin(r) = i / r = μ 

where μ ios refractive index of material of slab

Hence eqn.(2) becomes 

Hence factors affecting lateral displacement are (i) thickness of slab , (ii) angle of incidence and (iii) refractive index of material.

lateral displacement d is directly proportional to slab thckness t

lateral displacement d is directly proportional to angle of incidence i

lateral displacement increases as refractive index μ increases