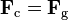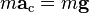CBSE Class 11-science Answered

For a geostationary satellite movin around the earth, calculate 1.Time period of revolution.2.Radius of parking orbit.3.Height from surfave of earth to satellite.

Asked by Vipul Kaushik | 19 Oct, 2010, 12:55: PM

Expert Answer

Dear Student

Geostationary satellites are located exactly above the earth’s equator and revolve around the earth in a circular orbit. Its revolving speed and direction (west to east) is exactly same as that of the earth, which makes it look stationary from the earth’s surface.

1. Time Period: Travels with a period equal to equal to the Earth's rotational period, i.e. one orbit takes 24 hours.

2. Radius of Parking orbit:

In any circular orbit, the centripetal force required to maintain the orbit is provided by the gravitational force on the satellite. To calculate the geostationary orbit altitude, one begins with this equivalence, and uses the fact that the orbital period is one sidereal day.

$\text{[math]}$

By Newton's second law of motion, we can replace the forces F with the mass m of the object multiplied by the acceleration felt by the object due to that force:

$\text{[math]}$

mass of the satellite m appears on both sides (gets cancelled)— geostationary orbit is independent of the mass of the satellite.

$\text{[math]}$ , $\text{[math]}$

gives, $\text{[math]}$ .

or $\text{[math]}$

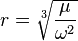
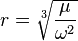
The angular speed ω is found by dividing the angle travelled in one revolution (360° = 2π rad) by the orbital period (the time it takes to make one full revolution: 86,164.09054 seconds).

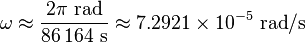
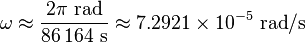
Gives, $\text{[math]}$

Hence r (orbital radius) = 42,164 kilometres.

3. Height from surface of Earth: Subtracting the Earth's equatorial radius, [6,378 kilometres] from the orbital radius gives the altitude of 35,786 kilometres.

Hope that satisfies your query.

Team

TopperLearning

Answered by | 19 Oct, 2010, 11:09: PM