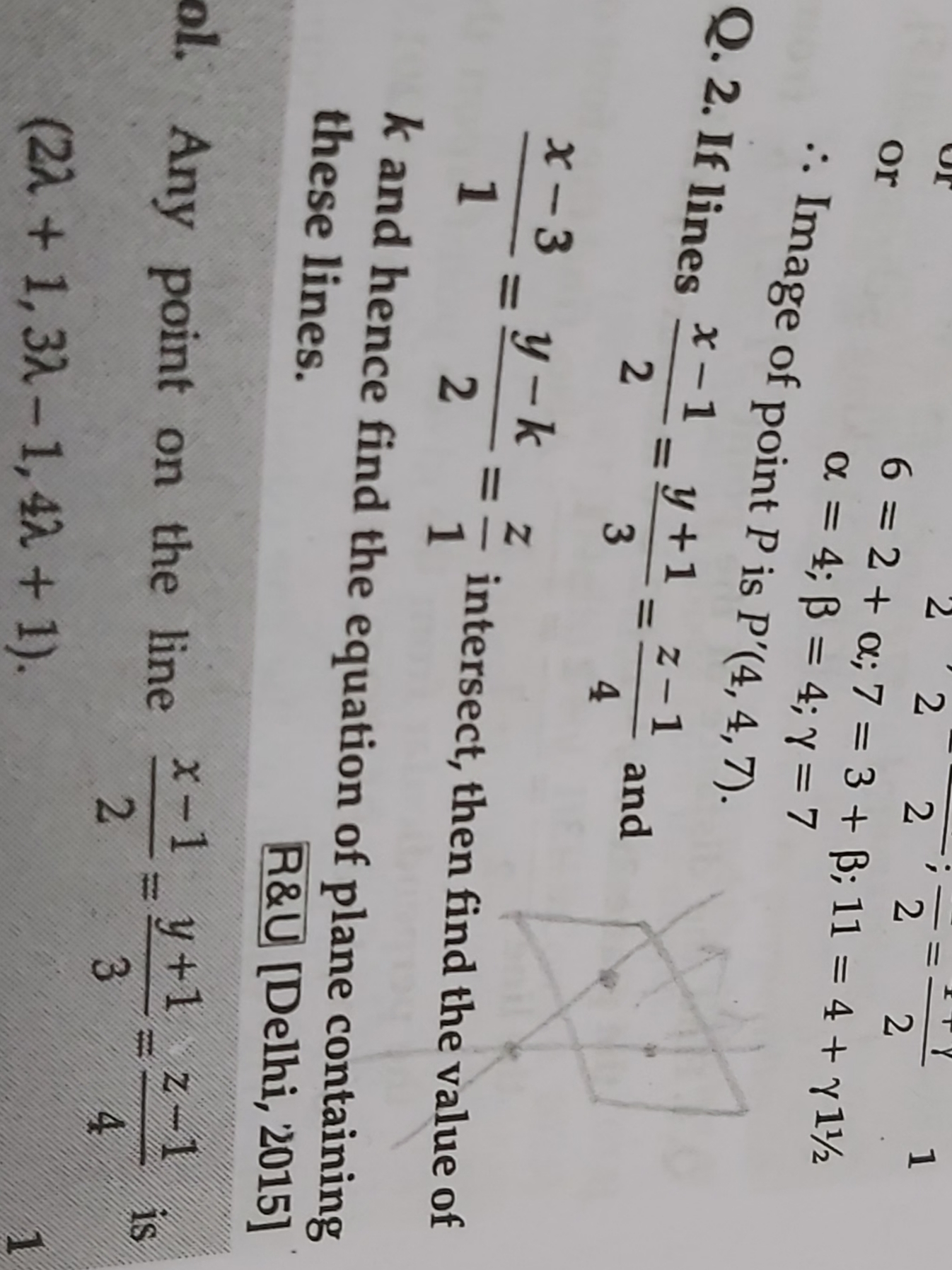CBSE Class 12-science Answered

 r1=(?-1) i+(?+1) j-(?+1) k, r2=(1-?) i+(2?-1)j+(?+2)k 

r1 = (-1, 1, -1) + ? (1, 1, -1)   and   r = (1, -1, 2) + ?(-1, 2, 1).

The point P with position vector p = (-1, 1, -1) lies on r1. 
The point Q with position vector q = (1, -1, 2) lies on r2 

The cross product of the two direction vectors, (1, 1, -1) and (-1, 2, 1) gives a common normal to both planes.

Working this out gives the vector (3,0,3).
So a unit normal vector to both planes is given by  1/3sqrt(2) (3, 0, 3). 
The equation of P(1) is  1/sqrt(13) (3, 0, 2) . r = 1/3sqrt(2) (3, 0, 3) . (-1, 1, -1) = -2/sqrt(2).
The equation of P(2) is  1/sqrt(13) (3, 0, 2) . r = 1/3sqrt(2) (3, 0, 3). (1, -1, 2) = 3/sqrt(2).
So the shortest distance between the 2 skew lines is |-2/sqrt(2) -3/sqrt(2) | = 5sqrt(2)/2 units.