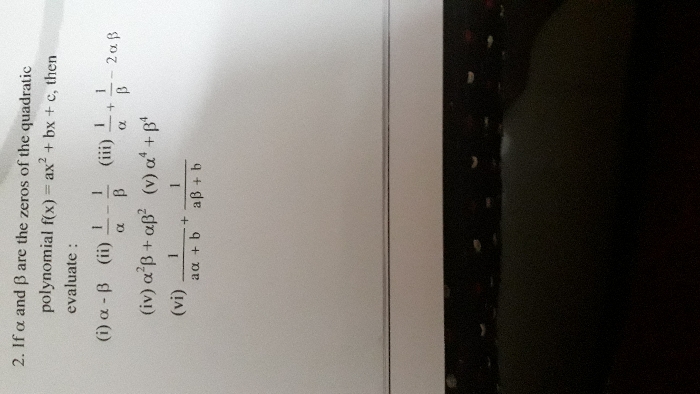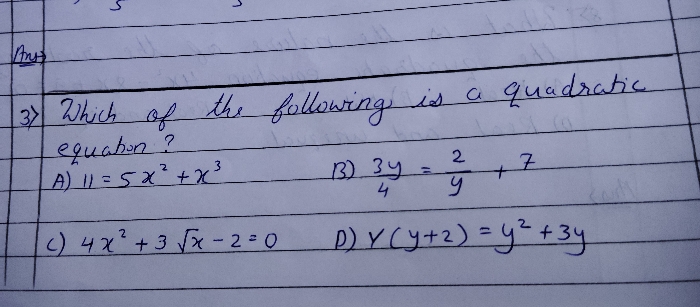Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

find the con
question image
Asked by mdkingofficial786 | 21 Dec, 2020, 04:37: PM
answered-by-expert Expert Answer
Question: Find the condition such that difference of the roots of the equation ax2 + bx + c = 0 is equal to the product of the roots.
Solution:
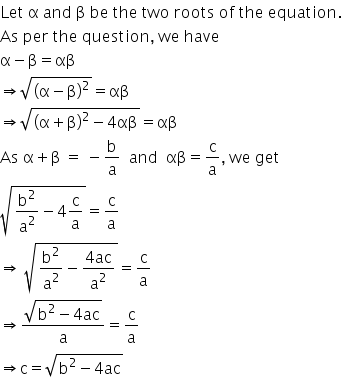
Let space straight alpha space and space straight beta space be space the space two space roots space of space the space equation. As space per space the space question comma space we space have straight alpha minus straight beta equals αβ rightwards double arrow square root of open parentheses straight alpha minus straight beta close parentheses squared end root equals αβ rightwards double arrow square root of open parentheses straight alpha plus straight beta close parentheses squared minus 4 αβ end root equals αβ As space straight alpha plus straight beta space equals space minus straight b over straight a space space and space space αβ equals straight c over straight a comma space we space get square root of straight b squared over straight a squared minus 4 straight c over straight a end root equals straight c over straight a rightwards double arrow space square root of straight b squared over straight a squared minus fraction numerator 4 ac over denominator straight a squared end fraction end root equals straight c over straight a rightwards double arrow fraction numerator square root of straight b squared minus 4 ac end root over denominator straight a end fraction equals straight c over straight a rightwards double arrow straight c equals square root of straight b squared minus 4 ac end root
Answered by Renu Varma | 22 Dec, 2020, 11:09: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
maths quadratic
question image
Asked by afiyamallick12 | 23 Feb, 2024, 11:32: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
If α and β are tge zeros of the polynomial x^2 - 6x + k and 3α + 2β=20 , then the value of k is
Asked by ruchipandey20071978 | 21 May, 2023, 10:00: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
What is a quadratic equation.
Asked by varma.renu9481 | 25 Jan, 2023, 04:11: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
hi
question image
Asked by chaudahryanshika | 03 Jan, 2023, 10:04: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
if alpha and bita are the zeroes of a quadratic polynomial X^2+X-2 then find the value of(1/alpha -1/bita)
Asked by devchauhan25007 | 17 Jul, 2022, 04:29: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
write (x-2)-x=3x(x-2) in the form of quadratic equation
Asked by sdiyashika | 12 Apr, 2022, 03:07: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
if X square + 2K x kx + 4 4 is equal to zero has a root x is equal to 2 find the value of k
Asked by hazelvermah | 19 Apr, 2021, 09:02: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
find the con
question image
Asked by mdkingofficial786 | 21 Dec, 2020, 04:37: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
please clear
question image
Asked by rajvarshneytushar | 24 Sep, 2020, 12:44: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Derivation of quadritic formula
Asked by Uppalrakesh71 | 10 Apr, 2020, 03:38: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×