CBSE Class 11-science Answered
explain newton's equations of motion in graph method and nermarically
Asked by bhallan.kuldeep | 25 Jul, 2019, 20:28: PM
Expert Answer
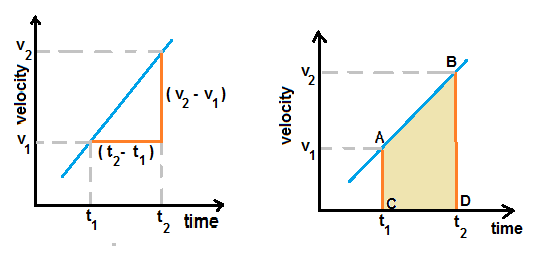
Fig.1 shows the velocity-time graph of uniformly accelerated motion.
Acceleration is defined as rate of change of velocity. Hence for instantaneous acceleration for a given point of motion,
we need to find slope of the velocity-time graph at the required point. For uniformly accelerated motion, acceleration is
constant, hence slope is constant. As per the plotted graph in fig.1, Let us consider a body which is moving with
velocity v1 at an instant of time t1 .
Let v2 be the velocity at time t2 . As shown in figure, slope = acceleration a = ( v2 - v1 )/( t2 - t1 ) ................(1)
Let us put, initial velocity v1 = u and final velocity v2= v and time duration (t2 - t1) = t,
Then from eqn.(1), a = (v-u)/t or we get v = u+a t ............................(2)
We know that area under the velocity-time graph is the distance travelled.
In fig.2, which is a velocity-time graph of uniformly accelerated motion, point-A represents the state of motion at time t1
when the velocity is v1 . Similarly point-B represents the state of motion at time t2 when the velocity is v2 .
Area of trapezium ABCD equals the distance travelled between time t1 and time t2 .
Area of trapezeium = (1/2)[ AC+BD ]×CD = (1/2)[v1 + v2 ]×(t2 - t1 ) ....................(3)
In eqn.(3), if we put, initial velocity v1 = u , final velocity = v and time duration (t2 - t1 ) = t
then we get , Area of trapezium = distance S = (1/2)( v + u )×t .....................(4)
if we substitute for final velocity v from eqn.(2), then we have, S = (1/2) (u+at+u)×t = u t + (1/2) a t2 ................(5)
In eqn.(4), if we substitute for t from eqn.(2), we get, S = (1/2)(v+u) [ (v-u)/a ] = (1/2) [ v2 - u2 ] / a
Hence, v2 = u2 + 2 a S ......................... (6)
Answered by Thiyagarajan K | 26 Jul, 2019, 13:51: PM
Concept Videos
-
Units and Measurement
This video explains the international unit system, parallax method of measu... -
Units and Measurement
This video explains significant figures, rules to identify significant figu... -
Units and Measurement
This video explains unique features of the clock at Jantar Mantar, units us... -
Units and Measurement
This video explains dimensions of physical quantities, dimensional formulae... -
Units and Measurement
This video contains practice questions on measuring large distances, measur...
CBSE 11-science - Physics
Asked by barunmandal12345jmt | 11 Jul, 2024, 16:23: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by chandinichauhai | 10 Jul, 2024, 23:32: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by sulthanxx | 08 Jul, 2024, 19:29: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by bhuvana.s3001 | 21 Jun, 2024, 23:21: PM
ANSWERED BY EXPERT
CBSE 11-science - Physics
Asked by contact.asmita03 | 15 Jun, 2024, 11:51: AM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by parthjain2448 | 12 Jun, 2024, 15:53: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by kaivalyaam | 12 Jun, 2024, 03:24: AM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by tkanmani022 | 11 Jun, 2024, 20:50: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by duraisamysteephen | 08 Jun, 2024, 12:32: PM
ANSWERED BY EXPERT
