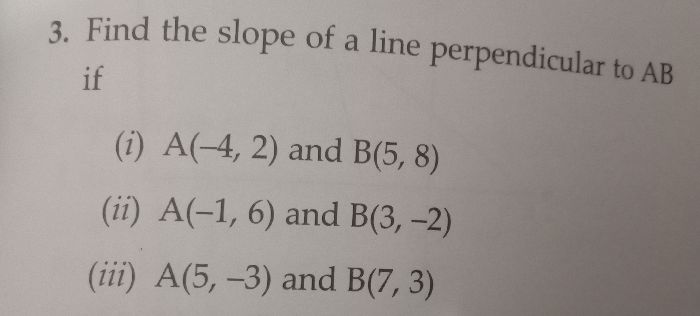ICSE Class 10 Answered
ex. 12 A q3
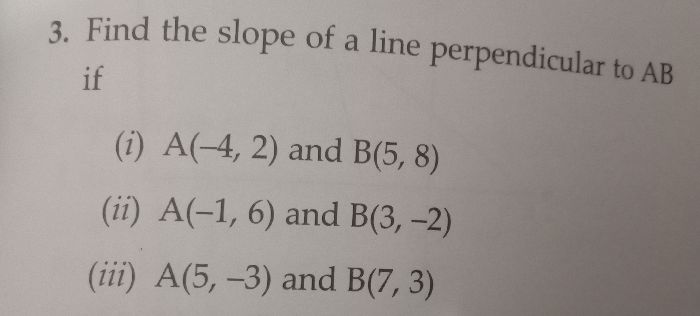
Asked by nilesh.dhote74 | 07 May, 2020, 10:22: PM
Expert Answer
To find the slope of a line perpendicular to AB if
(i) A(-4, 2) and B(5, 8)
(ii) A(-1, 6) and B(3, -2)
(iii) A(5, -3) and B(7, 3)
Solution:
(i)
Slope of AB = (y2-y1)/(x2-x1) = (8-2)/[5-(-4)] = 6/9 = 2/3
Slope of a line perpendicular to AB = -1/Slope of AB = -1/(2/3) = -3/2
(ii)
Slope of AB = (y2-y1)/(x2-x1) = (-2-6)/[3-(-1)] = -8/4 = -2
Slope of a line perpendicular to AB = -1/Slope of AB = 1/2
(iii)
Slope of AB = (y2-y1)/(x2-x1) = [3-(-3)]/[7-5] = 6/2 = 3
Slope of a line perpendicular to AB = -1/Slope of AB = -1/3
Answered by Renu Varma | 08 May, 2020, 11:49: AM
Concept Videos
-
Slope of a Straight Line
This video explains how to find the slope of a line, condition for parallel... -
Concepts on slope of a line
Slope of a line and Condition for parallelism and perpendicularity of lines... -
Slope of a Line ...
This video explains how to find the slope of a line, condition for parallel... -
Equation of A Line
Equation of A Line, Slope of A Line
ICSE 10 - Maths
Asked by nilesh.dhote74 | 18 May, 2020, 09:22: PM
ANSWERED BY EXPERTICSE 10 - Maths
Asked by nilesh.dhote74 | 17 May, 2020, 10:09: PM
ANSWERED BY EXPERTICSE 10 - Maths
Asked by nilesh.dhote74 | 08 May, 2020, 10:11: PM
ANSWERED BY EXPERT
ICSE 10 - Maths
Asked by sonali | 23 Feb, 2018, 11:19: AM
ANSWERED BY EXPERTICSE 10 - Maths
Asked by hajerianvi2002 | 19 Feb, 2018, 11:38: PM
ANSWERED BY EXPERTICSE 10 - Maths
Asked by lovemaan5500 | 18 Jan, 2018, 01:16: PM
ANSWERED BY EXPERT
