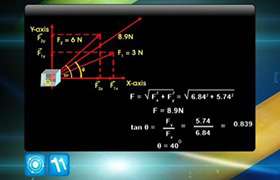
CBSE Class 11-science Answered
A particle possesses two velocities at the same time one 4 m/s due south and other the 2√2 m/s due north- east. Find the magnitude and direction of resultant velocity.
Asked by aditya.loya9821 | 08 Jul, 2021, 09:13: AM
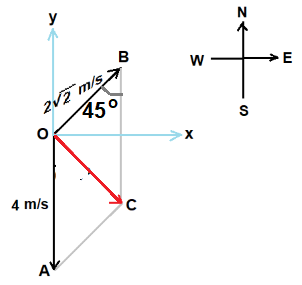
Velocity components 4 m/s and 2√2 m/s acting on the object are shown in figure.
Resultant velocity is detrmined by parallelogram method .
Let velocity components OA = 4 m/s and OB = 2√2 m/s are two adjacent sides of parallelogram as shown in figure.
Let us make the parallelogram OACB with adjacent sides OA and OB as shown in figure.
Diagonal OC is resultant velocity that is determined using cosine formula from ΔOBC
OC2 = OB2 + BC2 - (2 × OB × BC × cos45)
OC2 = 8 + 16 - ( 2 × 4 × 2√2 × cos45 ) = 8
Hence , OC = √8 m/s = 2√2 m/s
Since OB = OC , we get  OBC =
OBC =  OCB =
OCB =  AOC = 45o
AOC = 45o
 OBC =
OBC =  OCB =
OCB =  AOC = 45o
AOC = 45oHence magnitude of resultant = 2√2 m/s and direction is South-East
------------------------------------------------------------------------
Resultant OC is determined by vector method as explained below
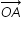 = - 4
= - 4 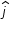 m/s
m/s 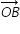 = ( 2
= ( 2  + 2
+ 2 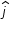 ) m/s
) m/s  and
and 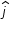 are unit vectors along x-axis and y-axis direction
are unit vectors along x-axis and y-axis directionResultant 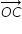 =
= 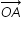 +
+ 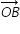 = ( 2
= ( 2  - 2
- 2 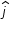 ) m/s
) m/s
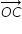 =
= 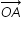 +
+ 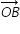 = ( 2
= ( 2  - 2
- 2 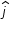 ) m/s
) m/sMagnitude of resultant = | 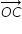 | = ( 22 + 22 )1/2 m/s = 2√2 m/s .
| = ( 22 + 22 )1/2 m/s = 2√2 m/s .
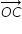 | = ( 22 + 22 )1/2 m/s = 2√2 m/s .
| = ( 22 + 22 )1/2 m/s = 2√2 m/s .Direction of resultant = tan-1 ( uy/ ux ) = tan-1 ( -2/ 2 ) = -45o ,
Where uy is y-component of resultant and ux is x-component of resultant
i.e. resultant velocity makes angle 45o with x-axis in clockwise direction .
Hence direction of resutlat is South-East
Answered by Thiyagarajan K | 08 Jul, 2021, 12:51: PM
Concept Videos
CBSE 11-science - Physics
Asked by vinitdubey7735 | 14 Mar, 2024, 11:21: AM
CBSE 11-science - Physics
Asked by dhanshreekansyakar | 09 Jan, 2024, 11:57: AM
CBSE 11-science - Physics
Asked by banhisikhapanda49 | 07 Nov, 2023, 10:42: PM
CBSE 11-science - Physics
Asked by preethiprithivi05 | 21 Feb, 2023, 09:28: PM
CBSE 11-science - Physics
Asked by rk274268 | 05 Aug, 2022, 01:19: PM
CBSE 11-science - Physics
Asked by Kattaithihaas | 24 Jul, 2022, 01:23: PM
CBSE 11-science - Physics
Asked by pawankumardas15492 | 22 Jul, 2022, 10:24: PM
CBSE 11-science - Physics
Asked by nutankumari95074 | 11 Jun, 2022, 05:24: PM
CBSE 11-science - Physics
Asked by kaziryan.05 | 13 Apr, 2022, 09:01: PM