CBSE Class 10 Answered
A
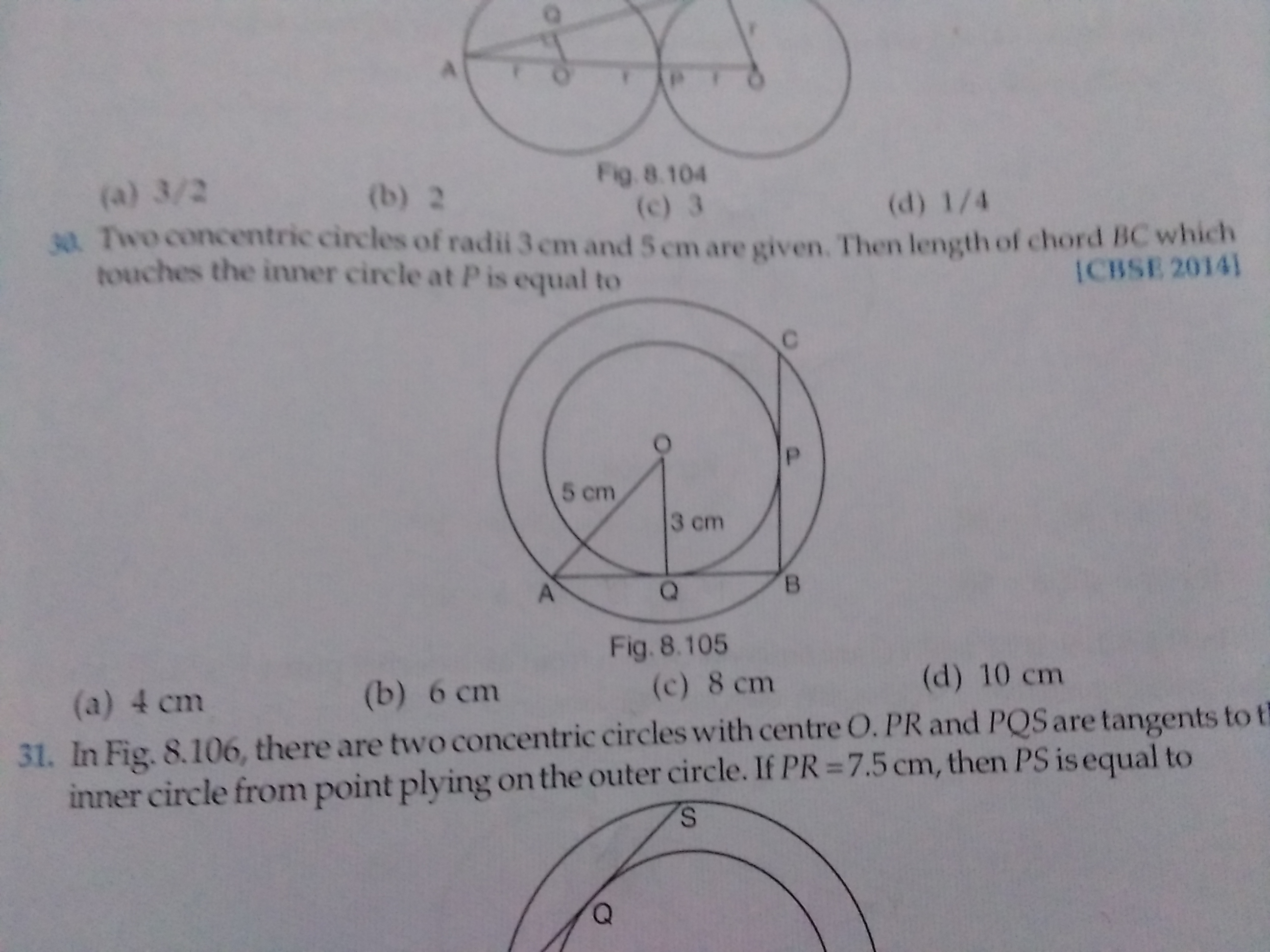
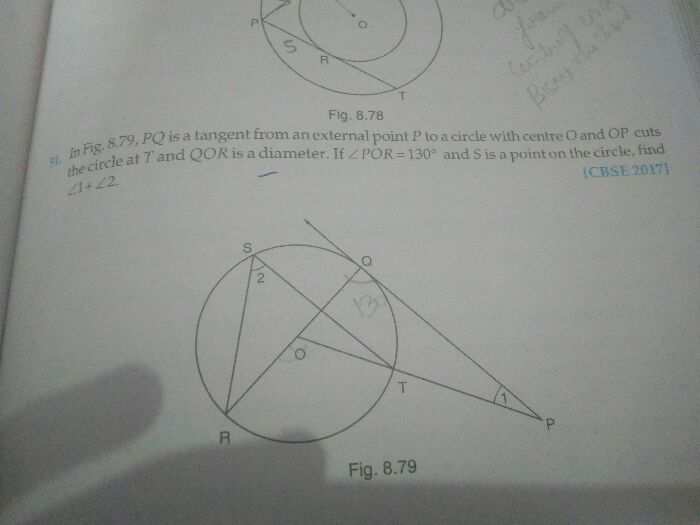
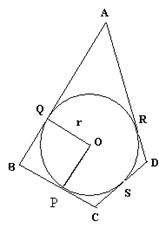
circle is inscribed in a quadrilateral ABCD in which  B = 90o. If AD = 23 cm, AB = 29 cm and DS =
5 cm. Find the radius of the circle.
B = 90o. If AD = 23 cm, AB = 29 cm and DS =
5 cm. Find the radius of the circle.

Asked by Topperlearning User | 27 Jul, 2017, 01:09: PM
Since tangents drawn from an external point to a circle are equal.
DR = DS = 5cm
Now, AR = AD - DR = 23 - 5 = 18cm
But, AR=AQ
![]() AQ
= 18cm
AQ
= 18cm
Also, BQ = AB - AQ = 29- 18 = 11cm
But, BP = BQ
![]() BP=11cm
BP=11cm
Also,
![]() Q=
Q=![]() P =90o.
P =90o.
In quadrilateral OQBP,
![]() QOP+
QOP+![]() P+
P+![]() Q+
Q+![]() B=360°
B=360°
![]() QOP
= 360° - (
QOP
= 360° - (![]() P+
P+![]() Q+
Q+![]() B)
B)
= 360° - (90°+90°+90°) = 90°
Hence, OQBP is a square.
![]() BQ=OQ=OP=BP=11cm
BQ=OQ=OP=BP=11cm
Hence, radius of the circle is 11cm.
Answered by | 27 Jul, 2017, 03:09: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by yalagondanikhil | 16 Apr, 2024, 12:25: PM
CBSE 10 - Maths
Asked by riazu945 | 16 Jan, 2022, 01:00: PM
CBSE 10 - Maths
Asked by sinhkaran79 | 14 Mar, 2021, 12:59: PM
CBSE 10 - Maths
Asked by s.saumya1011 | 05 Nov, 2020, 02:10: PM
CBSE 10 - Maths
Asked by brjkishorchauhan03 | 04 Nov, 2020, 12:10: PM
CBSE 10 - Maths
Asked by shivappahb308 | 21 Sep, 2020, 02:15: PM
CBSE 10 - Maths
Asked by VasupradUboveja376 | 22 Jun, 2020, 12:03: AM