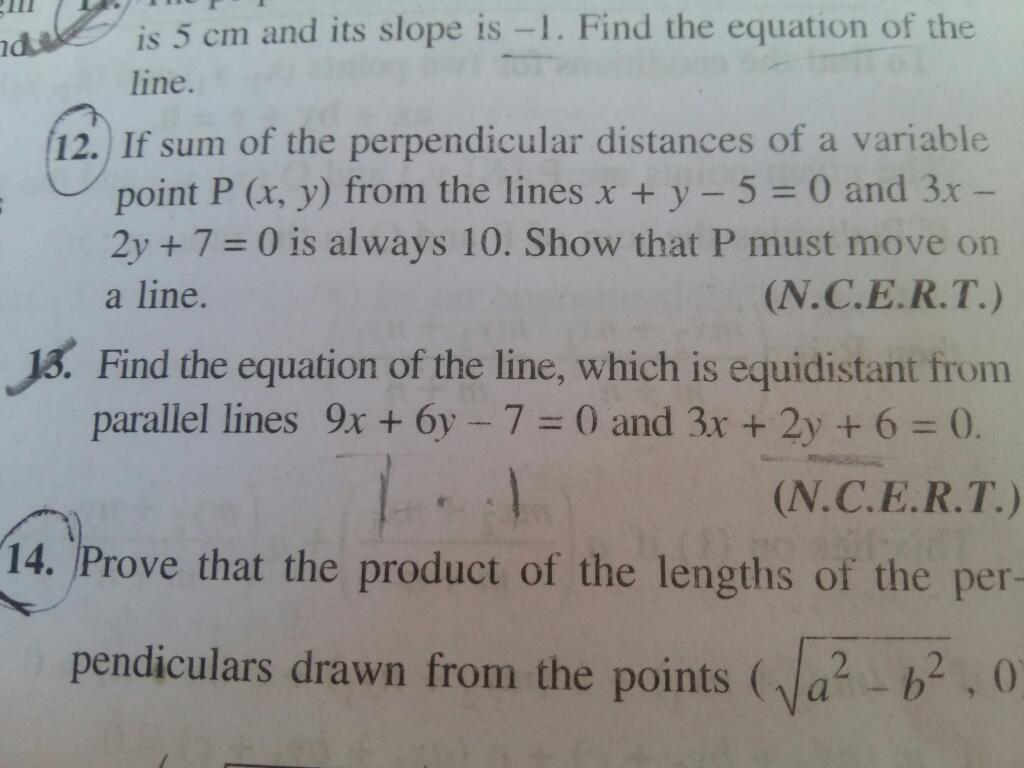CBSE Class 11-science Answered
14th sum plz
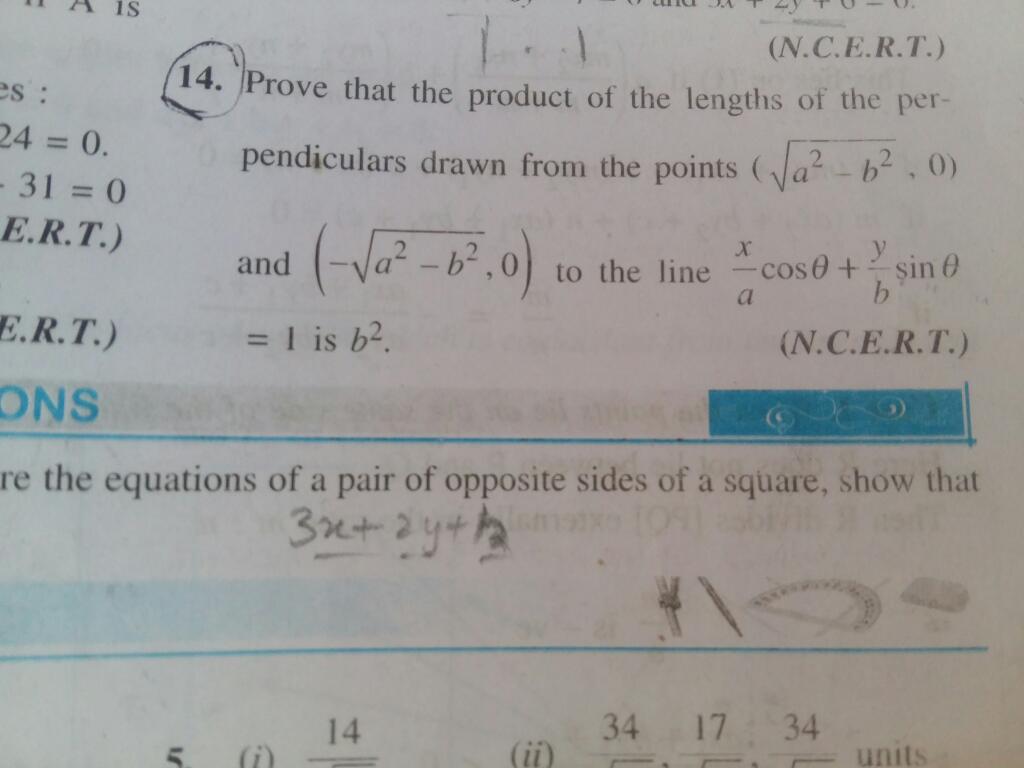
Asked by lovemaan5500 | 07 Oct, 2018, 14:35: PM
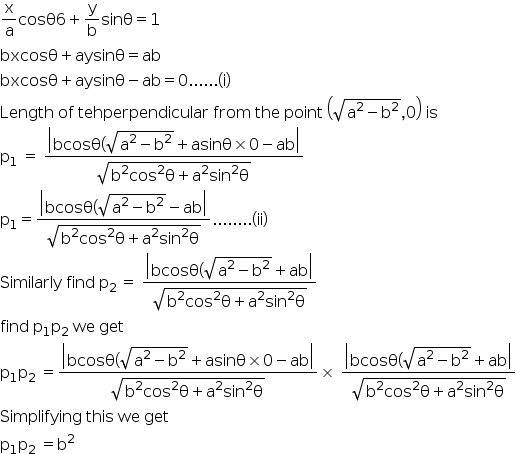
Answered by Sneha shidid | 08 Oct, 2018, 11:37: AM
Concept Videos
CBSE 11-science - Maths
Asked by lovemaan5500 | 08 Oct, 2018, 17:06: PM
CBSE 11-science - Maths
Asked by lovemaan5500 | 07 Oct, 2018, 14:35: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 30 Apr, 2014, 10:30: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 30 Apr, 2014, 10:30: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 29 Apr, 2014, 15:24: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 20 Oct, 2016, 07:13: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 30 Apr, 2014, 10:29: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 30 Apr, 2014, 10:31: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 30 Apr, 2014, 10:31: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 30 Apr, 2014, 10:33: AM