CBSE Class 11-science Answered

explain newton's equations of motion in graph method and nermarically

Asked by bhallan.kuldeep | 25 Jul, 2019, 08:28: PM

Expert Answer

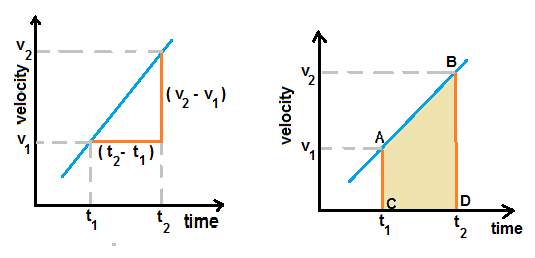
Fig.1 shows the velocity-time graph of uniformly accelerated motion.

Acceleration is defined as rate of change of velocity. Hence for instantaneous acceleration for a given point of motion,

we need to find slope of the velocity-time graph at the required point. For uniformly accelerated motion, acceleration is

constant, hence slope is constant. As per the plotted graph in fig.1, Let us consider a body which is moving with

velocity v₁ at an instant of time t_{1 .}

Let v₂ be the velocity at time t₂ . As shown in figure, slope = acceleration a = ( v₂ - v₁)/( t₂ - t₁) ................(1)

Let us put, initial velocity v₁ = u and final velocity v₂= v and time duration (t₂ - t₁) = t,

Then from eqn.(1), a = (v-u)/t or we get v = u+a t ............................(2)

We know that area under the velocity-time graph is the distance travelled.

In fig.2, which is a velocity-time graph of uniformly accelerated motion, point-A represents the state of motion at time t₁

when the velocity is v₁. Similarly point-B represents the state of motion at time t₂ when the velocity is v₂ .

Area of trapezium ABCD equals the distance travelled between time t₁ and time t₂ .

Area of trapezeium = (1/2)[ AC+BD ]×CD = (1/2)[v₁ + v₂ ]×(t₂ - t₁ ) ....................(3)

In eqn.(3), if we put, initial velocity v₁ = u , final velocity = v and time duration (t₂ - t₁ ) = t

then we get , Area of trapezium = distance S = (1/2)( v + u )×t .....................(4)

if we substitute for final velocity v from eqn.(2), then we have, S = (1/2) (u+at+u)×t = u t + (1/2) a t² ................(5)

In eqn.(4), if we substitute for t from eqn.(2), we get, S = (1/2)(v+u) [ (v-u)/a ] = (1/2) [ v² - u² ] / a

Hence, v² = u² + 2 a S ......................... (6)

Answered by Thiyagarajan K | 26 Jul, 2019, 01:51: PM

Please Login or Sign up to continue!