NEET Class neet Answered
answer

Asked by meenatoofansingh3 | 15 Apr, 2021, 06:16: PM
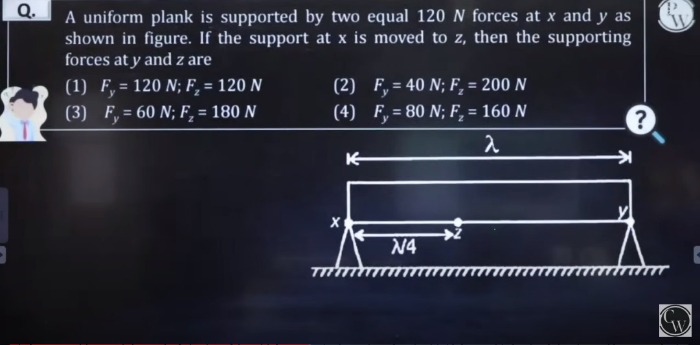
Qn.(6)
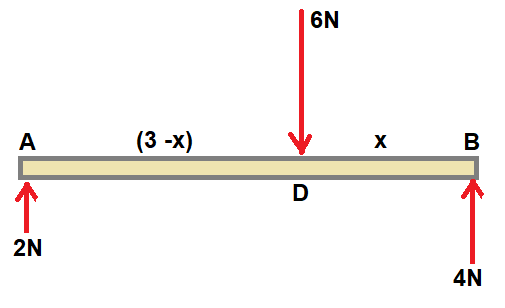
Let us consider 6N force is acting at D so that BD = x and AD ( 3 - x )
At equilibrium, sum of moments of forces is zero.
Let us take moments of forces about the point D.
At equilibrium, we have , 2 ( 3 - x ) = 4 x
Frome above expression, we get x = 1
Answer :- 6N force acting downward at a point D so that BD = 1 m
-------------------------------------------------------------------------

Figure shows the tension force T acting along the string .
At the disk of mass M , tension force T is giving torque to rotate the disc with angular acceleration α
Hence we have, T × R = I α .....................(1)
where R is radius of Disc , I = (1/2) M R2 is the moment of inertia and M is mass of disc
Angular acceleration α = a / R ,
where a is linear accelertion at rim of disc that is same as acceleration of block of mass m
Hence we rewrite eqn.(1) as , T × R = (1/2) M R2 × ( a / R )
Hence we get , T = (1/2) M a ...........................(2)
At the block of mass m , by applying Newton's second law , we get
( m g ) - T = m a ...........................(3)
By adding eqn.(2) and (3) , we get acceleration as
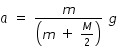 ..............................(4)
..............................(4)Hence , using eqn.(2) and (4) , we get tension T as
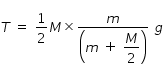 .......................(5)
.......................(5)Let us substitute values M = 2.4 kg , m = 1.2 kg , g = 9.8 m/s2
We get tension T = (1/2) × 2.4 × [ 1.2 / ( 1.2 + 1.2 ) ] × 9.8 = 5.88 N
Answered by Thiyagarajan K | 15 Apr, 2021, 09:44: PM
NEET neet - Physics
Asked by 69sayyappan | 29 Mar, 2024, 10:44: AM
NEET neet - Physics
Asked by anandibastavade555 | 24 Mar, 2024, 01:03: PM
NEET neet - Physics
Asked by snowgaming267 | 21 Mar, 2024, 01:44: PM
NEET neet - Physics
Asked by vikrantdhurdev2020 | 15 Mar, 2024, 04:10: PM
NEET neet - Physics
Asked by vijayyadav08735 | 20 Feb, 2024, 03:18: PM
NEET neet - Physics
Asked by meheboob1doctor | 21 Dec, 2022, 09:09: AM