CBSE Class 10 - Euclid's Division Lemma and Algorithm Videos
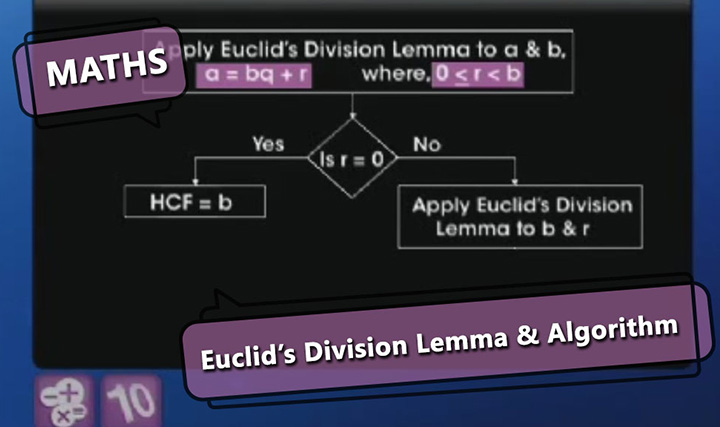
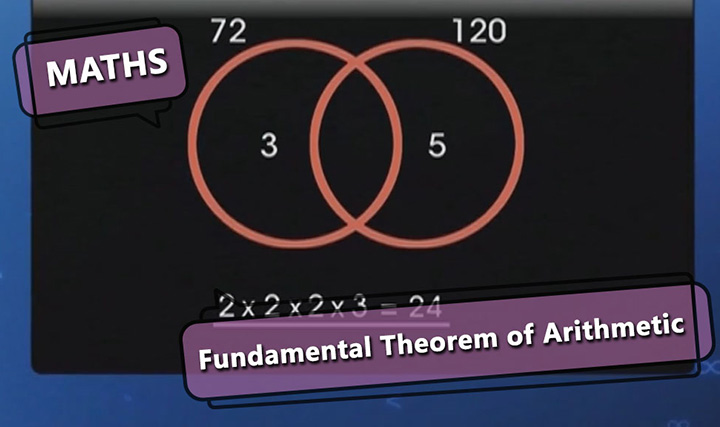
Euclid's Division Lemma and Algorithm
This video explains the statement of Euclid's Division lemma and algorithm and solves problems based on them.
More videos from this chapter
View All- What is réal number
- What is the HCF of 555 and 477
- the HCF of 867 and 255 is
- What is the HCF of the numbers 440 and 1782
- Find the LCM of 2³ × 3² and 2² × 3³.
- Find the smallest number which when divided by 45, 30, 60 having remainder 5 in each case.
-
a number n when divides by 16 gives the reminder 5 ______ is the reminder when the same number divide by 8

- find log27base3
- what is the meaning of uklid division
- what do you mean by h.c.f