CBSE Class 10 Maths Section Formula
- Points P and Q trisect the line segment joining the points A(– 2, 0) and B(0, 8) such that P is near to A. Find the coordinates of points P and Q.
- The coordinates of the point which divides the line segment joining the points(4,-3) and (8,5) in the ratio 3:1 internally is
- the foot of the perpendicular from P(-3,2) to y-axis I M. coordinates of M are....
- find the points which divide the line segments joining the points (1 , 7 ) (- 6 , - 3) in the ratio of 2:3
-
how to solve this

- . O is the origin. B( ?6, 9 ) and C ( 12, ?3) are the vertices of the ?ABC. If the ? point P divides OB in the ratio 1 ? 2 and the point Q divides OC in the ratio ? 1 ? 2. Show that PQ =1? 3? BC
- find the ratio in which the line 3x+4y+9=0 divides the line segment joining the line segments joining the points (1,3)(2,7)
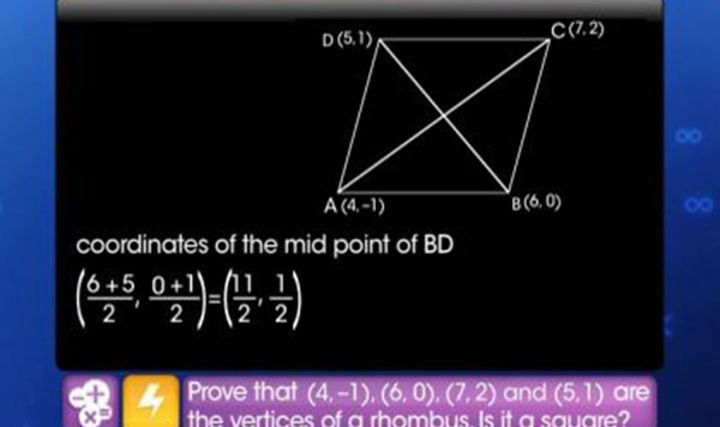
- The base BC of an equilateral triangle ABC lies on y?axis. The coordinates of point C are (0,–3).The origin is the midpoint of the base. Find the coordinates of the points A and B. Also, find the coordinates of another point D such that ABCD is a rhombus.
- line intersects the y-axis and x-axis at points P and Q respectively. If (2, -5) is the mid point of PQ, then find the coordinates of P and Q. So, x1=0.
- Find the coordinates of the points of trisection of the line segment joining (4,1) and (-2,-3).