Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

. O is the origin. B( −6, 9 ) and C ( 12, −3) are the vertices of the ∆ABC. If the  point P divides OB in the ratio 1 ∶ 2 and the point Q divides OC in the ratio  1 ∶ 2. Show that PQ =1 3 BC
Asked by pandurangaiah02 | 18 May, 2021, 12:01: PM
answered-by-expert Expert Answer
Given: O(0, 0), B(-6, 9), C(12, -3)
As P divides OB in the ratio 1 : 2, we have

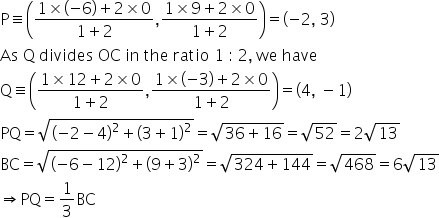
straight P identical to open parentheses fraction numerator 1 cross times open parentheses negative 6 close parentheses plus 2 cross times 0 over denominator 1 plus 2 end fraction comma fraction numerator 1 cross times 9 plus 2 cross times 0 over denominator 1 plus 2 end fraction close parentheses equals open parentheses negative 2 comma space 3 close parentheses As space straight Q space divides space OC space in space the space ratio space 1 space colon space 2 comma space we space have straight Q identical to open parentheses fraction numerator 1 cross times 12 plus 2 cross times 0 over denominator 1 plus 2 end fraction comma fraction numerator 1 cross times open parentheses negative 3 close parentheses plus 2 cross times 0 over denominator 1 plus 2 end fraction close parentheses equals left parenthesis 4 comma space minus 1 right parenthesis PQ equals square root of open parentheses negative 2 minus 4 close parentheses squared plus open parentheses 3 plus 1 close parentheses squared end root equals square root of 36 plus 16 end root equals square root of 52 equals 2 square root of 13 BC equals square root of open parentheses negative 6 minus 12 close parentheses squared plus open parentheses 9 plus 3 close parentheses squared end root equals square root of 324 plus 144 end root equals square root of 468 equals 6 square root of 13 rightwards double arrow PQ equals 1 third BC
Answered by Renu Varma | 21 May, 2021, 11:54: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
the foot of the perpendicular from P(-3,2) to y-axis I M. coordinates of M are....
Asked by raj.mehta2006 | 21 Feb, 2024, 11:23: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
find the points which divide the line segments joining the points (1 , 7 ) (- 6 , - 3) in the ratio of 2:3
Asked by lakshmidasari280 | 29 Jan, 2024, 07:44: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
how to solve this
question image
Asked by arikeraj | 04 Jul, 2022, 07:46: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
. O is the origin. B( −6, 9 ) and C ( 12, −3) are the vertices of the ∆ABC. If the  point P divides OB in the ratio 1 ∶ 2 and the point Q divides OC in the ratio  1 ∶ 2. Show that PQ =1 3 BC
Asked by pandurangaiah02 | 18 May, 2021, 12:01: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
find the ratio in which the line 3x+4y+9=0 divides the line segment joining the line segments joining the points (1,3)(2,7)  
Asked by mridul8989mantri | 10 Aug, 2020, 11:31: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
The base BC of an equilateral triangle ABC lies on y‐axis. The coordinates of point C are (0,–3).The origin is the midpoint of the base. Find the coordinates of the points A and B. Also, find the coordinates of another point D such that ABCD is a rhombus.
Asked by singhanil49171 | 14 Jul, 2020, 05:31: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
line intersects the y-axis and x-axis at points P and Q respectively. If (2, -5) is the mid point of PQ, then find the coordinates of P and Q. So, x1=0.
Asked by madhur2020 | 30 May, 2020, 11:12: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Find the coordinates of the points of trisection of the line segment joining (4,1) and (-2,-3).
Asked by kauraaaradhana | 29 Feb, 2020, 01:36: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
If (-1,3) ,(1,-1), (5,1) are he vertices off a triangle,find the length of its medians.
Asked by vanshjangir28 | 28 Feb, 2020, 09:48: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
The coordinates of a point A, where AB is diameter of a circle whose center is (2,3) and B is (1,4)? (a) (3,-10) (b) (-3,10) (c) (1,-10) (d) none of these 
Asked by ashleshathakur124 | 10 Feb, 2020, 09:36: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×