Techniques to solve questions based on probability (Coins & Dice)

Although the calculations in probability problems are very simple, the order of mathematical equations/statements is often long and confusing. But probability word problems appear frequently in the competitive exams, and so, it becomes important to know the right technique of solving these problems.

Basics of Probability 

Probability is the chance of occurrence of an event.

Events are any occurrences such as

• Going to a bookstore  
• Arranging words   
• Sitting on a red chair

The measure of uncertainty is called the theory of probability. The study of the theory of probabilities is of great mathematical interest and of equally great practical importance. Probability always lies between 0 and 1. This means, the value of probability can never be negative or greater than 1.

For any event, there are two possibilities—happening or not happening.

Probability of an event happening is denoted by P(E).

Probability of an event not happening is denoted by .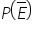

Note that P(E) +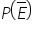 = 1.

There are two major types of events:

1. ‘AND’ event: Multiply or count events together (events happen together).

2. ‘OR’ event: Add events together (events happen separately).

 

Let’s illustrate this concept with a familiar model—the coin toss.

 

Coins

When a coin is tossed randomly, there are two possible outcomes—a head or a tail.

 

By the phrase ‘random toss’, we mean that the coin is allowed to fall freely without any bias or interference.

There are mainly three types of questions which can be asked on coins:

1. One coin tossed once

When a coin is tossed once, the total number of outcomes is

= (Possible cases: {H, T}) ^{(No. of trials)} = 2¹ = 2.

 

Q. What is the probability of getting a tail when a coin is tossed?

Number of favourable outcomes is 1.

So, the probability of getting a tail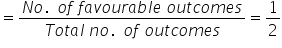 

Similarly, the probability of getting a head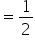

2. Two coins tossed together or one coin tossed twice

When two coins are tossed together or one coin is tossed twice, the following outcomes (each in order) are possible:

HH, HT, TH, TT (H = head and T = tail)

Total number of outcomes = (Possible cases: {H, T}) ^{(No. of trials)} = 2² = 4

 

Q. What is the probability of getting at least one head when two coins are tossed simultaneously?

Favourable outcomes are HH, HT and TH, as they contain at least one head.

Number of favourable outcomes = 3

So, the probability of getting at least one head

 

3. Three coins tossed together or one coin tossed thrice

When three coins tossed together or one coin tossed thrice, the following outcomes are possible:

HHH, HHT, HTH, HTT, THH, THT, TTH, TTT (H = head and T = tail)

Total number of outcomes = (Possible cases: {H, T}) ^{(No. of trials)} = 2³ = 8

 

Q. What is the probability of getting exactly two tails?

Favourable outcomes are HTT, THT and TTH, as they contain exactly two tails.

Number of favourable outcomes = 3.

So, the probability of getting exactly two tails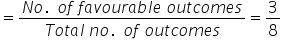

 

Dice

Dice are another mathematical model which feature in probability questions. The dice used here are the same as the ones we use to play Snakes & Ladders and Ludo. Each die has 1, 2, 3, 4, 5 and 6 written on its faces as shown below.

 

When a die is thrown, the number appearing on its upper face is the favourable outcome. And, just like in cricket, the favourite favourable outcome of most kids is 6!

Let’s get acquainted with the two main types of questions which can be asked on dice.

 

1. One die thrown once

When a die is thrown once, the following outcomes are possible:

1, 2, 3, 4, 5, 6

Total number of outcomes = 6

For every number, there is only one choice.

So, the probability of getting any number is .

Q. What is the probability of getting an odd number on rolling a die?

When a die is rolled, it shows either 1 or 2 or 3 or 4 or 5 or 6.

Total number of outcomes = 6

Odd numbers are 1, 3 and 5.

So, the number of favourable outcomes = 3

Therefore, the required probability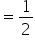

2. Two dice are thrown

In such cases, there are two possibilities—either two dice are thrown simultaneously and the numbers appearing on the dice are noted or one die is thrown two times and the numbers appearing on the die for both times are noted. In both of these cases, the outcomes are the same.

Various combinations of the numbers appearing on the dice are listed below:

(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)

(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)

(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)

(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)

(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)

(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)

Here (2, 1) means 2 appears on die 1 and 1 appears on die 2.

 

Q. If two dice are rolled, find the probability of getting a combination of 4 and 2.

Total number of possible outcomes = 36

Favourable outcomes are (2, 4) and (4, 2).

So, the number of favourable outcomes = 2

Therefore, the required probability .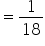

 

Q. If two dice are rolled, find the probability of getting the number 9 when the numbers are summed up.

Total number of possible outcomes = 36

To get the sum as 9, the possible combinations are (3, 6), (4, 5), (5, 4) and (6, 3) as .

So, the number of favourable outcomes = 4

Hence, the required probability = .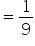

 

Please remember:

• To solve any question on probability, list the given and needed information so that you do not miss anything important.
• List the possible and favourable outcomes.
• Multiply when ‘AND’ is given and add when ‘OR’ is given.

 

Using these simple tricks, you can solve multiple problems based on probability.

The concept of probability is very easy to understand and is a part of both CBSE and ICSE board. Get Selina solutions for Class 10, NCERT solutions for Class 10, R.D.Sharma for Class 9, R.D.Sharma for Class10, R.D.Sharma for Class 11, R.S.Aggarwal for Class 9.

 

Start your new academic year with TopperLearning’s study resources. Get seamless access to sample papers, past years’ papers, most important questions, video lessons, mock tests, weekly tests and much more. Call our academic consultant on 9372462318 or visit TopperLearning.

 

CBSE Class 10 study resources

CBSE Class 12 Science study resources

CBSE Class 12 Commerce study resources

ICSE Class 10 study resources

JEE Main 2021 study resources

NEET 2021 study resources